Xinhua Lu , Hui Wan , Lingxiao Zhang , Hao Zhang and Zheng He
DFPINet: Dual Feature and Progressive Interaction Network for Point Cloud Registration
Abstract: In point cloud registration, the combination of global and local features provides a comprehensive representation of point cloud data. Previous registration methods predominantly relied on a single type of feature. For instance, correspondence matching-based methods require stringent criteria for the uniqueness of input point clouds, and the quality of feature extraction significantly influences the accuracy of registration results. Global feature-based methods capture the overall geometric information of the inputs; however, the absence of local information often leads to the neglect of the adverse effects caused by non-overlapping points. In this paper, we present DFPINet, an iterative network based on dual feature extraction and progressive feature interaction for partial-to-partial point cloud registration of small-scale object point clouds. We use a dual branch structure to individually extract both global and local features, fully utilizing the geometric characteristics of the point cloud. Additionally, the progressive feature interaction operation enhances feature connections and mitigates the effect of non-overlapping points. Experimental results demonstrate that our method surpasses existing registration approaches in both accuracy and robustness.
Keywords: Dual Feature , Partial-to-Partial , Point Cloud Registration , Progressive Feature Interaction
1. Introduction
Point cloud registration is a fundamental task in the field of computer vision, where the goal is to accurately align different point clouds to predict rigid transformations. Point cloud registration is extensively utilized in 3D reconstruction [1], simultaneous localization and mapping (SLAM) [2], and autonomous driving [3].
Iterative nearest point (ICP) [4] is a pioneering work, which determines the correspondence relationship based on the distance, and iteratively estimate the three-dimensional transformation through singular value decomposition (SVD). ICP and its various forms [5-7] were the most widely used methods in the early development of registration tasks. However, when confronted with partially overlapping point cloud scenarios, traditional registration methods often struggle to accurately identify overlapping regions within the point clouds, leading to a significant number of incorrect matches. This makes the registration task difficult to accomplish, and furthermore, these methods typically require substantial computational costs. Recently, some innovative works have proposed deep learning-based approaches for extracting feature descriptions from point clouds, such as PointNet [8] and dynamic graph convolutional neural network (DGCNN) [9]. Compared to traditional hand-crafted descriptors, these deep learning-based methods demonstrate superior robustness, higher computational efficiency, and the capability to extract high-level semantic information. As a result, learning based methods have emerged to handle registration problems.
Learning-based registration algorithms [10-15] can be broadly categorized into two types: correspondence matching based and global feature based methods. The deep closest point (DCP) [11] approach leverages the DGCNN for feature extraction and employs an attention module to determine correspondence. Furthermore, PRNet [13] and RPMNet [14] respectively employ Gumbel-Softmax [16] and Sinkhorn normalization [17] to determine the matching point pairs between the two input point clouds. These methods based on corresponding matching are heavily dependent on local geometric information from input point clouds, they focus solely on the salient local geometric information of the point clouds and fail to leverage the information of inputs. As a result, they often exhibit poor registration performance when dealing with point clouds lacking distinctive features.
The approaches of global feature based can capture the complete set features of point clouds by aggregating global information, such as PointNetLK [10], and feature-metric registration (FMR) [15], they utilize the PointNet network to extract global feature vectors from the point clouds and directly regress the transformation parameters using a multi-layer perceptron (MLP). This methods do not require salient local geometric features to determine point pair correspondences, relying solely on global feature vectors for the registration process. However, in partial-to-partial registration tasks, they generally overlook the adverse effects of non-overlapping regions. Therefore, for partially overlapping point cloud registration scenarios, fully utilizing the global and local information of point clouds and combining the advantages of multiple features to achieve high-precision registration still poses significant challenges.
In this paper, we propose DFPINet, an iterative registration network designed to achieve robust performance in the presence of noise. DFPINet extracts both global and local features from input point clouds, effectively leveraging their complementary structural information. Meanwhile, in order to promote the fusion of different features and interaction between point clouds, a two stages feature interaction process is introduced. Our primary contributions are summarized as follows:
· We propose a dual-branch feature extraction structure, which is used to parallelly extract global and local features from the source and reference point clouds. The introduction of these two types of features augment the representational capacity of feature descriptors, overcoming the limitations of relying solely on a single kind of feature.
· We propose a novel module for feature interaction, PFI (progressive feature interaction), which consists of two stages of interaction. The PFI facilitates the information interaction between global and local features of the inputs, as well as fusing feature vectors between different point clouds.
· We conducted multiple experiments to compare with other works on datasets with noisy and different overlapping ratios, indicating that DFPINet has excellent performance.
2. Related Work
2.1 Correspondence Matching based Methods
Most methods based on corresponding matching establish a relationship between the inputs, then calculate the transformation matrix. ICP [4] takes the nearest point pair between inputs as the corresponding point, and estimate point cloud transformation parameters using the SVD. ICP is highly sensitive to initialization, often getting stuck in local optima, and performs poorly when facing noise and outlier data. Subsequent improvements have addressed some of the aforementioned issues, Go-ICP [7] employs a branch-and-bound strategy to explore the transformation space, resulting in significantly reduced speed. Symmetric ICP [18] improves the point-to-plane objective function. To speed up iterations, fast global registration (FGR) [19] uses alternating optimization techniques.
Deep learning methods optimize point cloud feature extraction. DCP uses convolutional neural networks (CNN) to obtain feature descriptors, and establishes the corresponding relationship using attention mechanism. DeepGMR [12] combined with Gaussian mixture model to establish corresponding relationships. In conclusion, the primary challenge lies in the need for point clouds with unique geometric structure information, to facilitate the acquisition of sparse feature points. However, not all regions of a point cloud are unique, some similar regions can affect the establishment of matching relationships. Additionally, the predicted results are derived solely from sparse matched points, ignoring the non-matching points and not utilizing the global information of inputs.
2.2 Global Feature based Methods
The methods based on global features no longer focuses on establishing corresponding relationships, they extract global features from two inputs and employ end-to-end neural networks to estimate transformation. PointNetLK [10] is one of the earliest methods based on global feature, which use PointNet [8] to obtain global features, and employ Lucas and Kanade (LK) algorithm [20] to calculate point cloud transformation. To enhance robustness of PointNetLK against noise, PCRNet [21] uses fully connected layers to complete transformation regression. Furthermore, FMR uses an additional decoder to optimize the global feature distance of the point clouds. However, these algorithms all use PointNet as the encoder, which only focuses on the global structural information of the inputs, and difficult to handle situations where point clouds data is not perfectly aligned.
2.3 Partial-to-Partial Registration Methods
Most application scenarios are more suitable for using partial-to-partial registration, and some studies focus on it. Particularly, PRNet [13] employs self-supervised learning technology while uses Gumble-Softmax to enhance feature correspondence. RPMNet [14] applies Sinkhorn normalization and annealing strategy to obtain soft point correspondences. RGM [22] further utilizes deep graph to establish matches to reduce the impact of outliers. OMNet [23] estimates the overlapping masks, which has achieved excellent performance. Our work follows the partial-to-partial registration approaches [13,14, 23], focusing on handling small-scale object point registration problems through the dual feature and information correlation.
3. Method
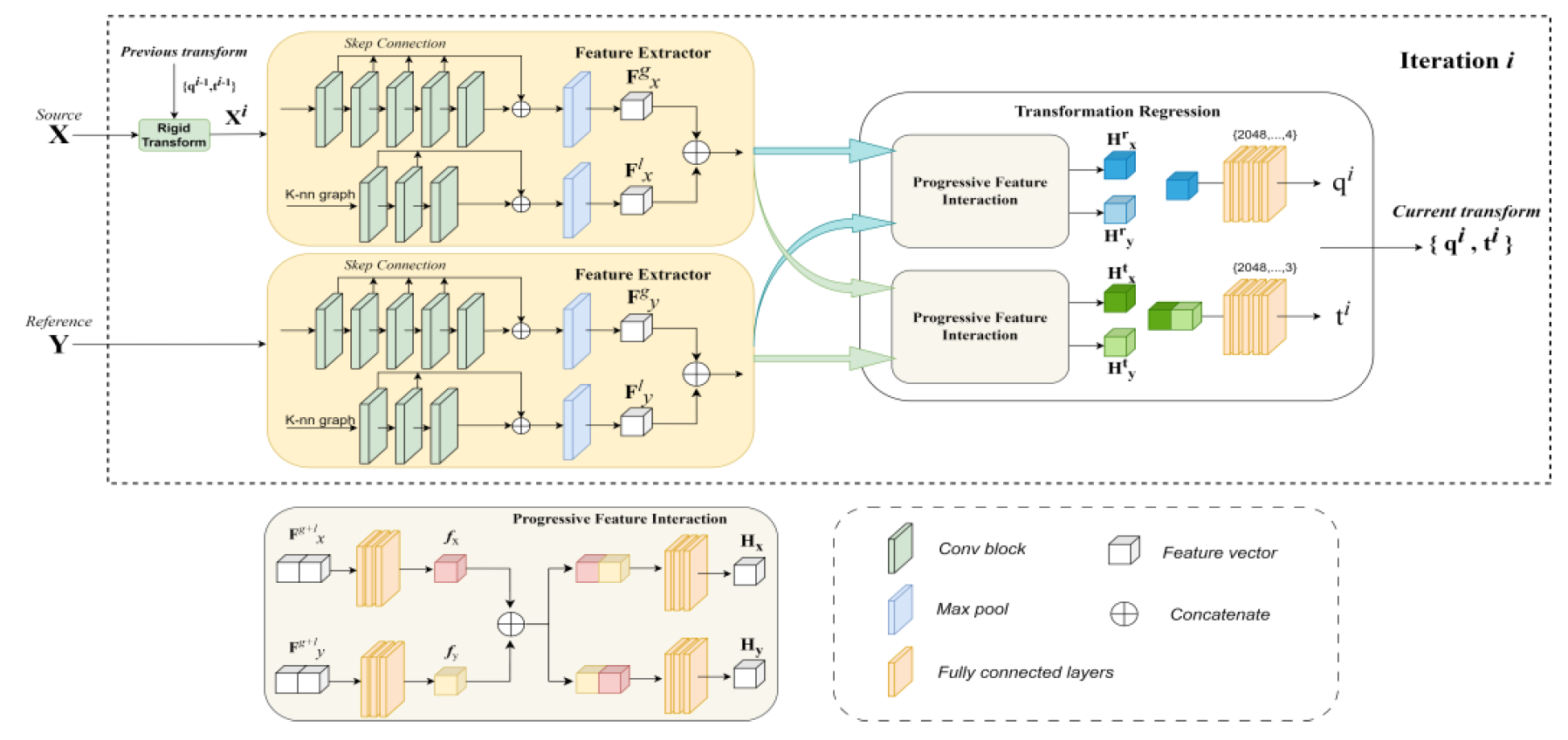
The workflow of DFPINet is shown in Fig. 1. At each iteration i, the 3D transformation comprises quaternion q and translation vector t. Using the rigid transformation [TeX:] $$\left\{q^{i-1}, t^{i-1}\right\}$$ estimated from the previous iteration, the source point cloud X is transformed to [TeX:] $$X^i$$. Subsequently, network extracts both global and local features from inputs. Next, the two features will be passed through the PFI module to interact between global and local features, as well as between the features of two inputs. Finally, the transformation regression module calculates the transformation [TeX:] $$\left\{q^i, t^i\right\}$$ for this iteration based on the previously obtained features, and calculate the loss of this iteration using loss function.
3.1 Feature Extraction
To simultaneously utilize the global structure and local details of point clouds, two encoder branches are designed in the feature extraction part, one for global feature extraction and the other focusing on local features of point clouds. In the global feature extraction branch, point-wise features produced by each convolution block are combined at multiple levels using max-pooling. At each iteration, X will be transformed into [TeX:] $$X^{\prime}$$ based on the results of the previous iteration process. Process of extracting global features is represented by the following equation:
In the local feature extraction branch, the k-nearest neighbor (KNN) algorithm is first applied, the input point clouds with dimension (3, N) are expanded to (3, N, k). Then, the matrix that contains the local information through convolutional layers to captures detail in data. The process of extracting local features is represented by the following equation:
(2)
[TeX:] $$G_m=K n n(m), \quad F_m^l=\max \left(\operatorname{cat}\left[{ }^k f_m^l \mid k=1 . . K\right]\right) .$$Here, [TeX:] $$m \in\left\{X^{\prime}, Y\right\} .$$ The k represents the number of convolutional layers, f is the point-wise features, K represents the number of convolutional blocks, channel-wise max-pooling is represented by [TeX:] $$\max (\cdot) \text{ and } \operatorname{cat}[\cdot ; \cdot]$$ means concatenation. [TeX:] $$G_m$$ is the set of points and their adjacent points in the inputs. Encoder is shared weights for the inputs.
3.2 Progressive Feature Interaction
For partial-to-partial registration, there exists non-overlapping regions between the inputs X and Y, which can interfere with the registration process. Therefore, the model needs to fully integrate global and local information to generate richer feature representations, while information association is required between two inputs.
We propose the PFI module to be used after feature extraction stage. The two kinds of features are first connected, followed by passing through MLPs to generate the fusion features, then combine the fusion features of X and Y and sent into MLPs to obtain interactive features. The entire process is defined as:
(3)
[TeX:] $$f_m=h_\theta\left(\operatorname{cat}\left[F_m^g, F_m^l\right]\right), \quad m \in\left\{X^{\prime}, Y\right\},$$
(4)
[TeX:] $$H_x=h_1\left(\operatorname{cat}\left[f_{X^{\prime}}, f_Y\right]\right), H_y=h_2\left(\operatorname{cat}\left[f_Y, f_{X^{\prime}}\right]\right).$$where [TeX:] $$h_\theta(\cdot)$$ denote the global and local feature fusion function in the first stage, [TeX:] $$h_1(\cdot) \text { and } h_2(\cdot)$$ denote the point cloud interaction function for source and reference point cloud.
3.3 Rigid Transformation Regression
The 3D rigid transformation performed by point clouds composed of translation and rotation, which have some degree of variation in their level of attention to various features. Therefore, we use two branches to regress the transformation parameters. Specifically, twice feature extraction of inputs by the network in the feature extraction stage, interactive features [TeX:] $$H_x \text { and } H_y$$ are generated for rotation and translation using PFI, respectively. The regression branchs take interactive features as input and produce two vectors, where 4D vector represents quaternion [TeX:] $$q \in R^4$$ and 3D vector represents translation vectors between point clouds as [TeX:] $$t \in R^3 .$$ In the parameter regression process, the transformation {q, t} is calculated as:
(5)
[TeX:] $$q=g_\theta^r\left(\operatorname{cat}\left[H_{x^{\prime}}^r, H_y^r\right]\right), t=g_\theta^t\left(\operatorname{cat}\left[H_{x^{\prime}}^t, H_y^t\right]\right) .$$Here, the function [TeX:] $$g_\theta^r(\cdot) \text { and } g_\theta^t(\cdot)$$ denote the rotation and translation regression networks.
3.4 Loss Function
Point cloud registration task requires continuously optimizing the predicted registration parameters to align two inputs, so it is necessary to measure deviation between ground truth and predicted transformation calculated by network. The regression loss of transformation at iteration i is as follows:
(6)
[TeX:] $$L=\frac{1}{N} \sum_{i=1}^N \lambda_1\left|q^i-q_{g t}\right|+\lambda_2\left\|t^i-t_{g t}\right\|_2$$where q and t indicate the quaternions and translation vector, gt indicate the ground truth. [TeX:] $$\lambda_1 \text { and } \lambda_2$$ are two hyperparameters that selects different values based on registration tasks to achieve better registration results. In this work, we set up [TeX:] $$\lambda_1=1, \lambda_2=4 .$$
3.5 Execution Flow
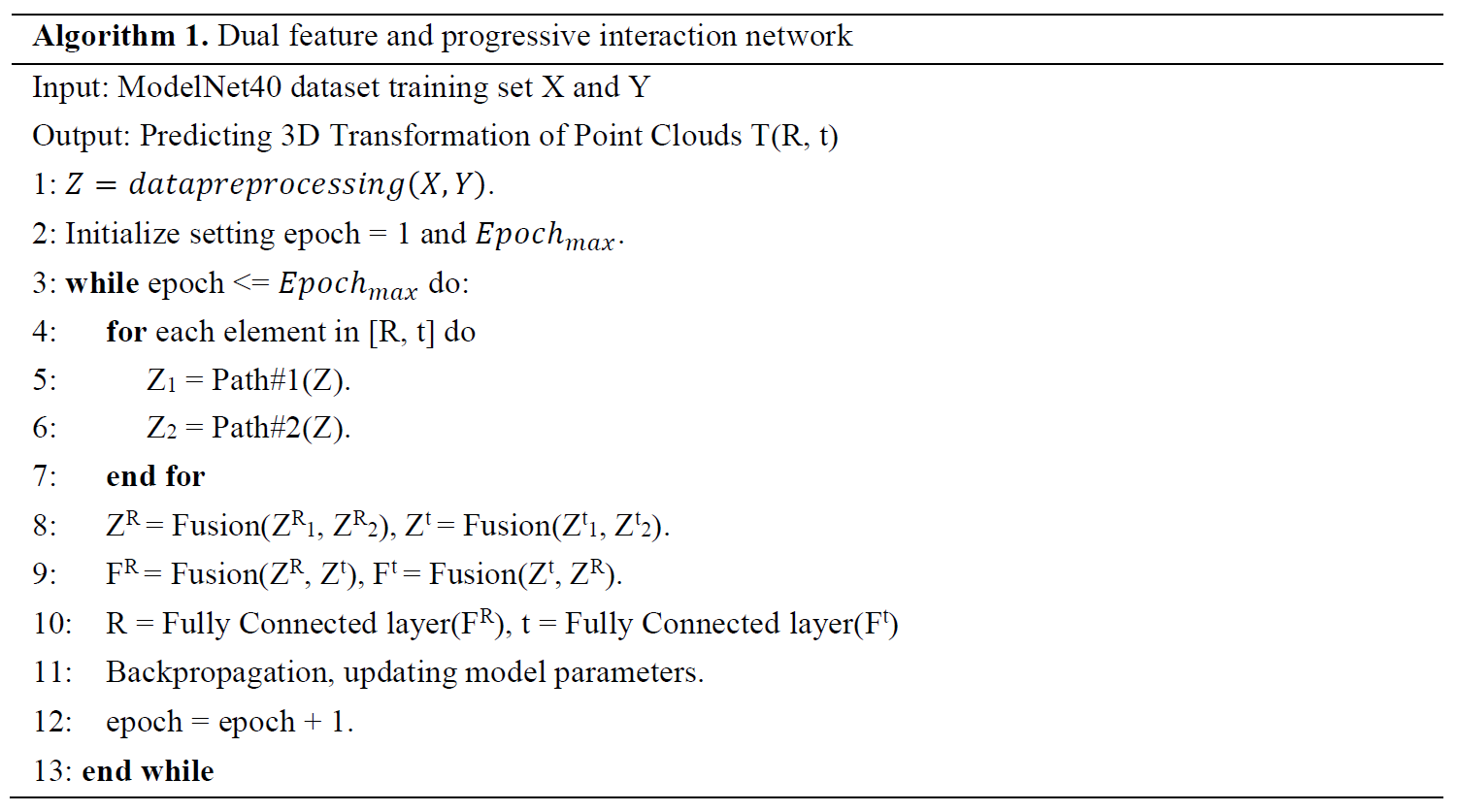
The detailed execution process of DFPINet is shown in Algorithm 1.
4. Experiments
4.1 Dataset and Implementation Details
Dataset: ModelNet40 [24] includes 40 categories of object CAD models. In realistic scenes, points in X are hard to find the exact correspondences in Y, but most previous works only sample point cloud once, which can lead to over-fitting issue. To reduce the impact of the above situation, we refer to OMNet, where separate sampling of the source and reference point cloud, and some axisymmetrical categories are removed. The processed data includes 4,196 training objects, 1,002 validation objects, and 1,146 testing objects. Following previous works [11,13,14], we arbitrarily produce rotations around three coordinate axes, each constrained within [[TeX:] $$0^{\circ}, 45^{\circ}$$], the alongside translations constrained within [-0.5,0.5] on three axis, to constitute the random transformation.
Implementation details: We set the number of iterations for the registration process to 4. We choose Adam optimizer and set learning rate [TeX:] $$\operatorname{lr}=10^{-4} .$$ The batch size is 16.
4.2 Baseline Algorithms
We compared DFPINet with other algorithms. Traditional algorithms include ICP, Symmetric ICP and FGR, ICP and FGR are implemented using Intel Open3D [25], while Symmetric ICP is implemented using point cloud library (PCL) [26]. Learning-based algorithms include PointNetLK, DCP, RPMNet, FMR, RGM, DeepGMR, and OMNet.
4.3 Evaluation Metrics
In this work, the evaluation metrics used are anisotropic error and isotropic error. Specifically, anisotropic errors are measured using root mean squared error (RMSE) and mean absolute error (MAE), comparing predicted values with the ground-truth values:
(7)
[TeX:] $$M S E=\sqrt{\frac{1}{N} \sum_{i=1}^n\left(V_{\text {gt }}-V_{\text {pred }}\right)^2}$$
where [TeX:] $$\left\{V_{\text {gt }}, V_{\text {pred }}\right\}$$ can be Euler angle pair or translation vector pair. To measure the registration result, we also use isotropic errors, which represent the errors between [TeX:] $$V_{g t} \text { and } V_{\text {pred }} .$$ The calculation process for these errors is as follows:
(9)
[TeX:] $$\operatorname{Error}(R)=\frac{1}{N} \sum_{i=1}^n \arccos \left(\frac{\operatorname{tr}\left(R_{g t} R_{p r e d}^{-1}\right)-1}{2}\right)$$
(10)
[TeX:] $$\operatorname{Error}(t)=\frac{1}{N} \sum_{i=1}^n\left\|t_{g t}-t_{\text {pred }}\right\|_2$$where gt represent the ground truth and pred is the predicted values, R means the rotation matrices and t means the translation vector. As the registration results improve, the values of (7)–(10) become smaller. All evaluation indicators related to rotation are measured in degrees.
4.4 Evaluation on ModelNet40
We conducted multiple experiments on different data to evaluate different methods. Data preprocessing settings are the same as RPMNet. Fig. 2 shows the visualization results.
Fig. 2.
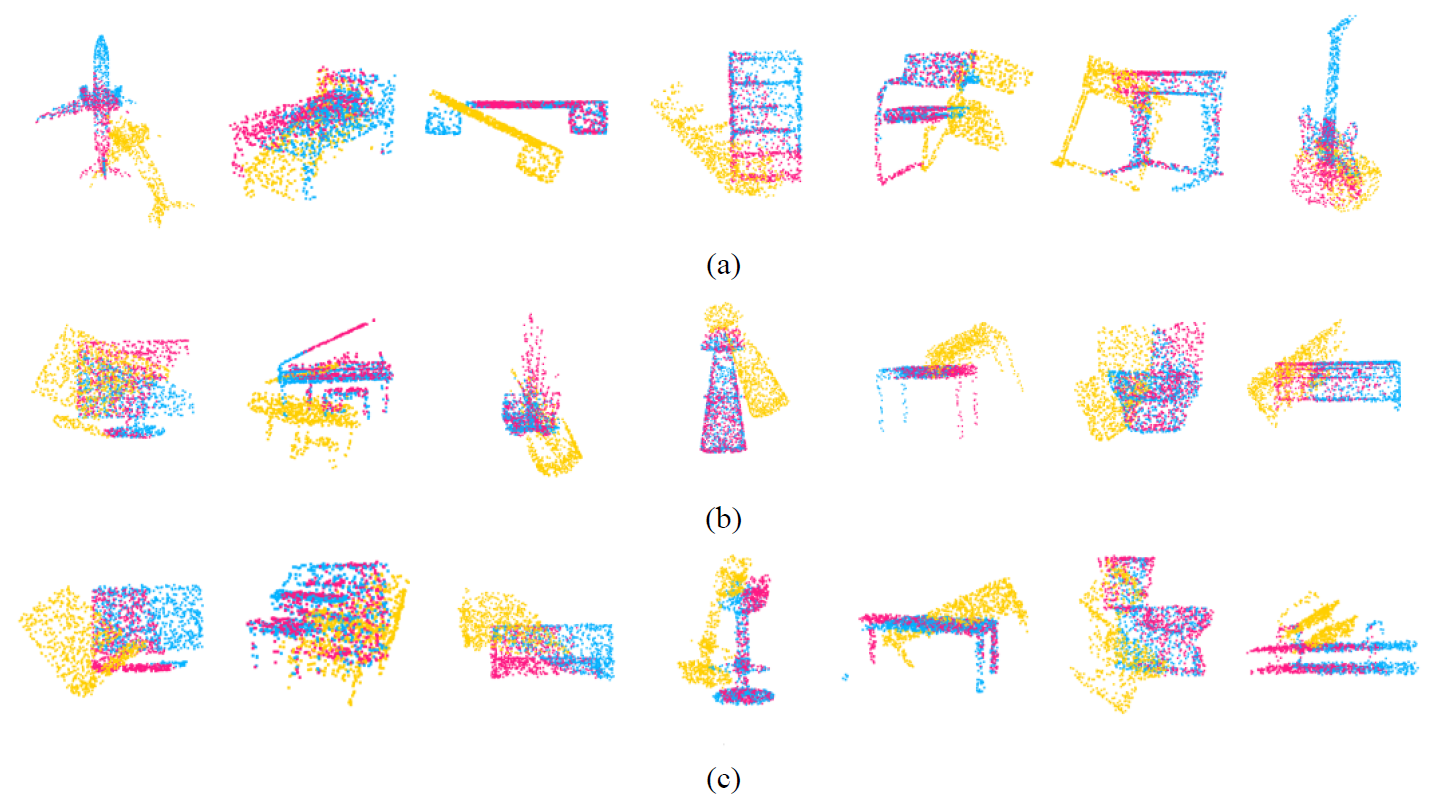
4.4.1 Unseen shapes
We used point cloud data from 14 categories to train the models, and evaluate the model using data of the same category as the training set. We cropped the input point clouds from 1,024 points to 717 points with a sampling rate of 70%, which is used in [14].
Table 1 shows the results. Traditional methods perform worse than learning based methods. ICP performs poorly due to significant initial position differences, while Symmetric ICP performs better. In addition, the down-sampling operations change the calculation manner of normal, resulting in poorer performance of FGR compared to ICP. Our method achieves superior registration performance over others.
4.4.2 Unseen categories
We evaluate the performance of DFPINet on unseen categories data. We test the model in categories different from the training set. Compared to the performance in Table 1, the performance of all learning-based methods has deteriorated as shown in Table 2. In contrast, traditional methods remain relatively stable due to their handmade features that are not susceptible to shape variations. Nevertheless, DFPINet continued to perform well on data from previously unseen categories.
Table 1.
| Method | RMSE(R) | MAE(R) | RMSE(t) | MAE(t) | Error(R) | Error(t) |
|---|---|---|---|---|---|---|
| ICP [4] | 22.840 | 12.147 | 0.1931 | 0.1217 | 24.654 | 0.2612 |
| Symmetric ICP [18] | 11.295 | 9.592 | 0.1394 | 0.1124 | 19.571 | 0.2414 |
| FGR [19] | 46.766 | 29.635 | 0.3041 | 0.2078 | 57.685 | 0.4263 |
| PointNetLK [10] | 27.482 | 18.627 | 0.2532 | 0.1778 | 36.947 | 0.3691 |
| DCP [11] | 11.109 | 8.454 | 0.0851 | 0.0599 | 9.216 | 0.1259 |
| FMR [15] | 8.033 | 4.999 | 0.1187 | 0.0726 | 9.741 | 0.1617 |
| RPMNet [14] | 2.162 | 1.135 | 0.0267 | 0.0141 | 2.280 | 0.0302 |
| RGM [22] | 4.912 | 1.786 | 0.0428 | 0.0183 | 3.506 | 0.0393 |
| OMNet [23] | 1.781 | 0.852 | 0.0341 | 0.0141 | 1.693 | 0.0299 |
| Proposed method | 1.735 | 0.687 | 0.0237 | 0.0110 | 1.402 | 0.0236 |
The bold font indicates the best performance in each test.
Table 2.
| Method | RMSE(R) | MAE(R) | RMSE(t) | MAE(t) | Error(R) | Error(t) |
|---|---|---|---|---|---|---|
| ICP [4] | 22.906 | 13.599 | 0.1994 | 0.1286 | 26.819 | 0.2700 |
| Symmetric ICP [18] | 12.333 | 10.746 | 0.1456 | 0.1186 | 21.437 | 0.2521 |
| FGR [19] | 41.644 | 26.193 | 0.2872 | 0.1951 | 51.463 | 0.4003 |
| PointNetLK [10] | 42.777 | 28.969 | 0.3210 | 0.2258 | 53.307 | 0.4613 |
| DCP [11] | 12.507 | 9.414 | 0.1020 | 0.0730 | 12.102 | 0.1493 |
| FMR [15] | 6.465 | 7.109 | 0.1330 | 0.0837 | 13.827 | 0.1817 |
| RPMNet [14] | 7.491 | 2.403 | 0.0579 | 0.0258 | 4.635 | 0.0556 |
| RGM [22] | 7.298 | 2.259 | 0.0624 | 0.0234 | 4.474 | 0.0511 |
| OMNet [23] | 4.881 | 2.256 | 0.0582 | 0.0268 | 4.437 | 0.0567 |
| Proposed method | 4.912 | 2.182 | 0.0539 | 0.0259 | 4.308 | 0.0557 |
The bold font indicates the best performance in each test.
Table 3.
| Method | RMSE(R) | MAE(R) | RMSE(t) | MAE(t) | Error(R) | Error(t) |
|---|---|---|---|---|---|---|
| ICP [4] | 21.893 | 13.402 | 0.1963 | 0.1278 | 26.632 | 0.2679 |
| Symmetric ICP [18] | 12.576 | 10.987 | 0.1478 | 0.1203 | 21.807 | 0.2560 |
| FGR [19] | 46.213 | 30.116 | 0.3034 | 0.2141 | 58.968 | 0.4364 |
| PointNetLK [10] | 29.733 | 21.154 | 0.2670 | 0.1937 | 42.027 | 0.3964 |
| DCP [11] | 12.730 | 9.556 | 0.1072 | 0.0774 | 12.173 | 0.1586 |
| FMR [15] | 11.674 | 7.400 | 0.1364 | 0.0867 | 14.121 | 0.1870 |
| RPMNet [14] | 6.160 | 2.463 | 0.0618 | 0.0274 | 4.913 | 0.0589 |
| RGM [22] | 6.893 | 3.068 | 0.0650 | 0.0311 | 6.243 | 0.0662 |
| OMNet [23] | 5.151 | 2.619 | 0.0566 | 0.0285 | 4.981 | 0.0605 |
| Proposed method | 5.110 | 2.310 | 0.0564 | 0.0269 | 4.577 | 0.0578 |
The bold font indicates the best performance in each test.
4.4.3 Gaussian noise
This experiment examined the robustness of DFPINet to noise. We used the same data from Section 4.4.2 for testing, and add Gaussian noise N(0, 0.012) to each point, clipping it to [-0.05,0.05]. As shown in Table 3, noise has negatively impacted the performance of all methods, with learning-based methods are more affected. The DFPINet is less affected by noise and performs well with robustness.
4.4.4 Summary of comparative experiments
Through the above three sets of comparative experiments, we can find that most deep learning-based registration methods have better registration performance than traditional registration methods. This is because feature extraction based on neural networks can obtain feature descriptors with stronger representation ability, and these feature descriptors are usually less susceptible to outliers and noise interference, making them more robust. Compared to other deep learning-based registration methods, our method achieved the best results in all three experiments. The dual feature extraction branch structure fully learns the global and local feature information of the point cloud, enabling the network to fully extract the available geometric information of the point cloud when facing partially overlapping point cloud data. The fused features generated through two stages of feature interaction enable the input point clouds to perceive each other's geometric structures, allowing the network to adapt to different data scenarios under different conditions.
4.5 Ablation Studies
We performed ablation studies using the same dataset as in Section 4.4.3 to validate and demonstrate the efficacy of our various components. We used the dual feature extraction module and the PFI module as variables to test their respective effects on the network. It should be noted that in the operation of removing the dual feature extraction module, we only retain the convolutional layer to extract global features, while changing the output dimension of the convolution to ensure that the final feature dimension is the same as before. Table 4 shows the experimental results. Comparing the second and third lines with the first line, we observe that all the components enhance the performance.
For translation registration, the translation operation primarily alters the spatial arrangement of point cloud data in 3D space. Local features capture the geometric relationships among neighboring points. The incorporation of local features enables the identification of corresponding local structures between two point clouds, facilitating the estimation of the translation vector. For rotation registration, the rotation operation reorients the point cloud data, necessitating broader contextual information to accurately determine the point clouds' orientation. The interrelationships within the data enable the network to more precisely determine the orientation of the point clouds, thereby enhancing the performance of rotation registration.
Table 4.
| Studies No. | Dual feature | PFI | Error(R) | Error(t) |
|---|---|---|---|---|
| 1 | 5.350 | 0.0664 | ||
| 2 | ✓ | 5.118 | 0.0620 | |
| 3 | ✓ | 4.898 | 0.0632 | |
| 4 | ✓ | ✓ | 4.577 | 0.0578 |
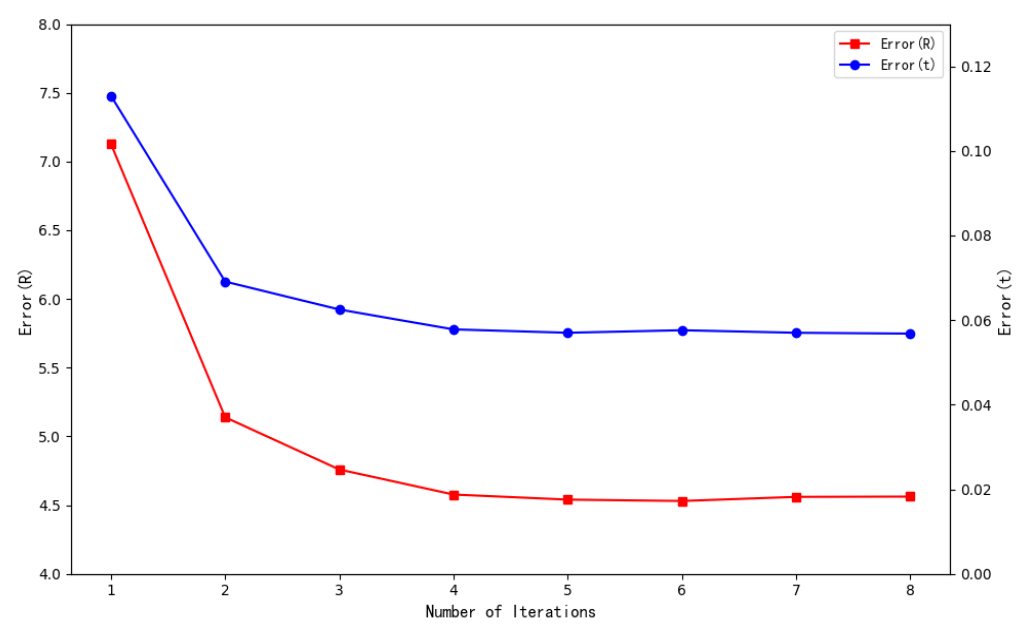
4.6 Number of Iterations
Point cloud registration generally requires multiple iterations. Generally, the registration accuracy will be higher with the increase of iterations. On the contrary, the inference time of the network will increase. To find the appropriate number of model iterations, this experiment used data with added noise and recorded isotropic rotation and translation errors within the range of 1–8 iterations. Fig. 3 shows the curve of error variation with the iterations. An observable fact is that the error remains stable at the beginning of the fourth iteration. Therefore, in all experiments of this article, the iterations is uniformly set to 4.
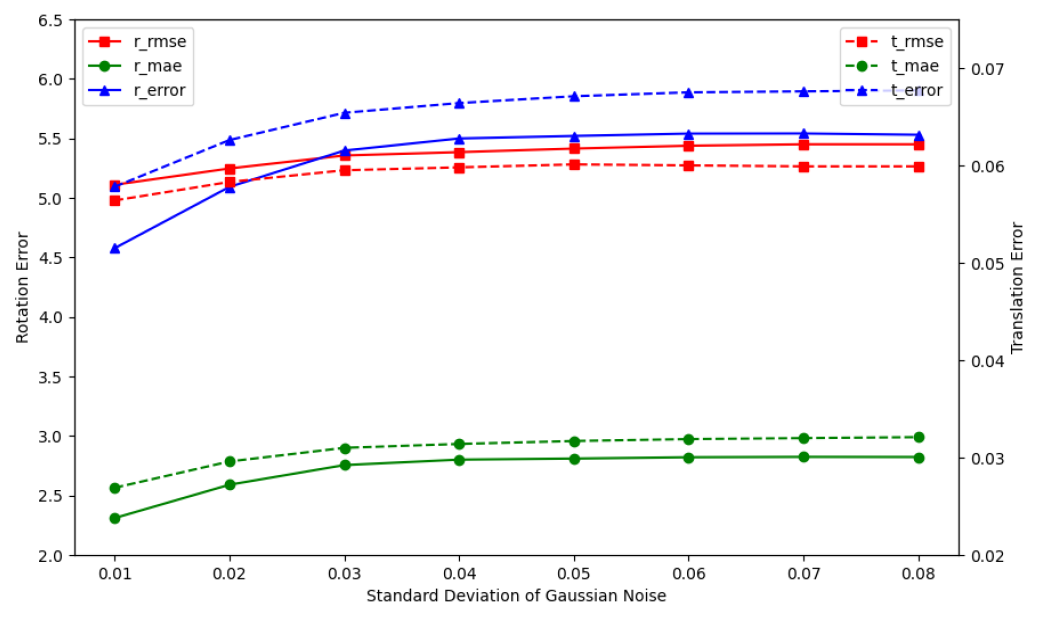
4.7 Robustness against Noise
We conducted tests at different noise levels to further validate the robustness of DFPINet against noise, we add noise following a N(0,[TeX:] $$\sigma^2$$) distribution, clipped to the range [-0.05,0.05]. Fig. 4 shows the results, various errors in registration vary slightly under different levels of noise. Our method has achieved excellent performance at different noise levels.
4.8 Different Overlap Ratios
To further test the processing ability of DFPINet for point clouds with different overlapping ratios, we randomly removed 10%–50% of points within the test set, tested different integrity data using the experimental parameter in Section 4.4.3. Table 5 presents that as integrity of the point cloud decreases, registration accuracy also decreases. However, the registration accuracy fluctuates slightly within a certain overlap ratio range and can remain stable, indicating that DFPINet can handle low overlap point clouds well.
Table 5.
| Overlapping ratio | Error(R) | Error(t) |
|---|---|---|
| 50% | 6.268 | 0.1280 |
| 60% | 5.264 | 0.0820 |
| 70% | 4.577 | 0.0578 |
| 80% | 3.974 | 0.0492 |
| 90% | 3.498 | 0.0413 |
4.9 Generalization
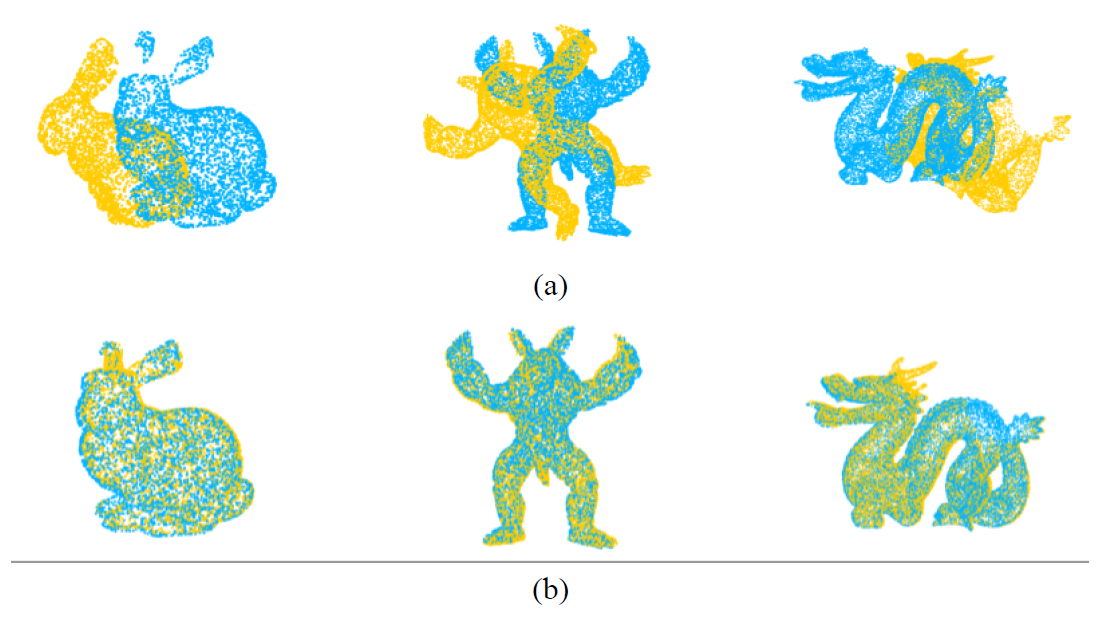
To better assess the generalization capability of DFPINet, we performed experiments with Stanford 3D Scan dataset [27]. The dataset only haves ten scanned object point clouds, we used DFPINet trained on ModelNet40 directly. Fig. 5 shows some registration results, where the first row displays the unaligned point clouds, and the second row shows the aligned point clouds after registration. This indicates that our model generalizes well across different datasets, highlighting its adaptability and effectiveness in real-world scenarios. The consistent performance further validates the robustness of DFPINet's architecture and its ability to handle diverse point cloud data.
5. Conclusion
We proposed DFPINet, an algorithm for partial-to-partial registration of small-scale object point clouds. Our method sends point clouds into a dual branch structure, extracting global and local features of point clouds separately, and designs a progressive feature interaction module to fully integrate different features and enhance information correlation between different point clouds. The experiment has demonstrated the effectiveness of DFPINet, and ablation studies have shown that the introduction of multiple features and sufficient information exchange can help enhance the precision of registration.
Despite its success with small-scale datasets, DFPINet exhibits lower registration accuracy when applied to large-scale datasets. This limitation highlights the need for further research to address the challenges posed by complex structural information in large-scale scenes. In future work, we plan to explore the integration of attention mechanisms to better capture intricate structural details in scene point cloud data. Additionally, we will investigate methods to enhance the algorithm's robustness to noise and its computational efficiency, which are critical for real-time applications.
Beyond these technical improvements, DFPINet holds significant potential for various practical applications, such as industrial quality inspection, autonomous driving, and medical imaging. By continuing to refine and expand the capabilities of DFPINet, we aim to contribute to the advancement of point cloud registration technologies and their adoption in real-world scenarios.
Funding
This paper was sponsored by Academic Degrees Graduate Education Reform Project of Henan Province (No. 2021SJGLX262Y and 2023SJGLX370Y), Postgraduate Education Reform and Quality Improvement Project of Henan Province (No. YJS2024AL141), and Foundation and frontier project of Nanyang (No. 24JCQY003).
Biography
Xinhua Lu
https://orcid.org/0000-0002-2338-7020He received the B.E., M.E., and Ph.D. degrees from Zhengzhou University, Zhengzhou, China, in 2003, 2007, and 2019 respectively. Since Sept. 2015, he was a visiting researcher in Department of Electronic Systems, Aalborg University for two years supported by China Scholarship Council. Now he is with Nanyang Institute of Technology, Nanyang, China, as an associate professor in the Academy for Electronic Information Discipline Studies. His main research interests include machine learning, Variational Bayesian Inference, and wireless communication.
Biography
Hui Wan
https://orcid.org/0009-0001-3823-6399He received the BS degree from the International College, Zhengzhou University, Zhengzhou, China, in 2022. He is currently pursuing the Master’s degree with the School of Computer and Artificial Intelligence, Zhengzhou University, Zhengzhou, China. His main research interest includes artificial intelligence and 3D point cloud registration.
Biography
Lingxiao Zhang
https://orcid.org/0009-0000-9638-8414He received the BE and ME degrees from Zhengzhou University and Wuhan University of Technology in 1996 and 2007 respectively. Since 1996, he has been with Nanyang Institute of Technology, Nanyang, China, where he is currently a professor with the School of Computer and Software. His research interest includes computer theory and deep learning techniques.
Biography
Hao Zhang
https://orcid.org/0009-0002-2784-1355He received the BS degree from the School of Information Engineering, Tianjin University of Commerce, Tianjin, China, in 2022. He is currently pursuing a master's degree in the School of Computer and Artificial Intelligence, Zhengzhou University, Zhengzhou, China. His main research interest is artificial intelligence and computer vision.
Biography
Zheng He
https://orcid.org/0009-0005-6732-9446He received the Master’s degree in Electronic and Information Engineering from Beijing University of Posts and Telecommunications in 2012, and is currently working as an engineer at China United Network Communication Group Co. Ltd., Nanyang Branch. His research interest includes deep learning techniques and wireless communication.
References
- 1 M. Merickel, "3D reconstruction: the registration problem," Computer Vision, Graphics, and Image Processing, vol. 42, no. 2, pp. 206-219, 1988. https://doi.org/10.1016/0734-189X(88)90164-8doi:[[[10.1016/0734-189X(88)90164-8]]]
- 2 J. Zhang and S. Singh, "LOAM: lidar odometry and mapping in real-time," in Proceedings of the 2014 Robotics: Science and Systems Conference, Berkeley, CA, USA, 2014. https://doi.org/10.15607/RSS.2014. X.007doi:[[[10.15607/RSS.2014.X.007]]]
- 3 A. Geiger, P. Lenz, and R. Urtasun, "Are we ready for autonomous driving? the KITTI vision benchmark suite," in Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 2012, pp. 3354-3361. https://doi.org/10.1109/CVPR.2012.6248074doi:[[[10.1109/CVPR.2012.6248074]]]
- 4 P. J. Besl and N. D. McKay, "Method for registration of 3-D shapes," in Proceedings of SPIE 1611: Sensor Fusion IV: Control Paradigms and Data Structures. Bellingham, WA: International Society for Optics and Phtonics, 1992, pp. 586-606. https://doi.org/10.1117/12.57955doi:[[[10.1117/12.57955]]]
- 5 S. Rusinkiewicz and M. Levoy, "Efficient variants of the ICP algorithm," in Proceedings of the 3rd International Conference on 3-D Digital Imaging and Modeling, Quebec City, Canada, 2001, pp. 145-152. https://doi.org/10.1109/IM.2001.924423doi:[[[10.1109/IM.2001.924423]]]
- 6 A. W. Fitzgibbon, "Robust registration of 2D and 3D point sets," Image and Vision Computing, vol. 21, no. 13-14, pp. 1145-1153, 2003. https://doi.org/10.1016/j.imavis.2003.09.004doi:[[[10.1016/j.imavis.1153.09.004]]]
- 7 J. Yang, H. Li, and Y . Jia, "Go-ICP: solving 3D registration efficiently and globally optimally," in Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 2013, pp. 1457-1464. https://doi.org/10.1109/ICCV .2013.184doi:[[[10.1109/ICCV.2013.184]]]
- 8 C. R. Qi, H. Su, K. Mo, and L. J. Guibas, "PointNet: deep learning on point sets for 3D classification and segmentation," in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 2017, pp. 77-85. https://doi.org/10.1109/CVPR.2017.16doi:[[[10.1109/CVPR.2017.16]]]
- 9 Y . Wang, Y . Sun, Z. Liu, S. E. Sarma, M. M. Bronstein, and J. M. Solomon, "Dynamic graph CNN for learning on point clouds," ACM Transactions on Graphics (TOG), vol. 38, no. 5, article no. 146, 2019. https://doi.org/10.1145/3326362doi:[[[10.1145/3326362]]]
- 10 Y . Aoki, H. Goforth, R. A. Srivatsan, and S. Lucey, "PointNetLK: robust & efficient point cloud registration using PointNet," in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 2019, pp. 7163-7172. https://doi.org/10.1109/CVPR.2019.00733doi:[[[10.1109/CVPR.2019.00733]]]
- 11 Y . Wang and J. M. Solomon, "Deep closest point: Learning representations for point cloud registration," in Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, South Korea, 2019, pp. 3523-3532. https://doi.org/10.1109/ICCV .2019.00362doi:[[[10.1109/ICCV.2019.00362]]]
- 12 W. Yuan, B. Eckart, K. Kim, V . Jampani, D. Fox, and J. Kautz, "DeepGMR: learning latent Gaussian mixture models for registration," in Computer Vision – ECCV 2020. Cham, Germany: Springer, 2020, pp. 733-750. https://doi.org/10.1007/978-3-030-58558-7_43doi:[[[10.1007/978-3-030-58558-7_43]]]
- 13 Y . Wang and J. M. Solomon, "PRNet: self-supervised learning for partial-to-partial registration," 2019 (Online). Available: https://arxiv.org/abs/1910.12240.doi:[[[https://arxiv.org/abs/1910.12240]]]
- 14 Z. J. Yew and G. H. Lee, "RPM-Net: robust point matching using learned features," in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 2020, pp. 1182111830. https://doi.org/10.1109/CVPR42600.2020.01184doi:[[[10.1109/CVPR42600.2020.01184]]]
- 15 X. Huang, G. Mei, and J. Zhang, "Feature-metric registration: a fast semi-supervised approach for robust point cloud registration without correspondences," in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 2020, pp. 11363-11371. https://doi.org/10.11 09/CVPR42600.2020.01138doi:[[[10.11 09/CVPR42600.2020.01138]]]
- 16 E. Jang, S. Gu, and B. Poole, "Categorical reparameterization with gumbel-softmax," 2016 (Online). Available: https://arxiv.org/abs/1611.01144v1.doi:[[[https://arxiv.org/abs/1611.01144v1]]]
- 17 R. Sinkhorn, "A relationship between arbitrary positive matrices and doubly stochastic matrices," The Annals of Mathematical Statistics, vol. 35, no. 2, pp. 876-879, 1964.custom:[[[-]]]
- 18 S. Rusinkiewicz, "A symmetric objective function for ICP," ACM Transactions on Graphics (TOG), vol. 38, no. 4, article no. 85, 2019. https://doi.org/10.1145/3306346.3323037doi:[[[10.1145/3306346.3323037]]]
- 19 Q. Y . Zhou, J. Park, and V . Koltun, "Fast global registration," in Computer Vision – ECCV 2016. Cham, Germany: Springer, 2016, pp. 766-782. https://doi.org/10.1007/978-3-319-46475-6_47doi:[[[10.1007/978-3-319-46475-6_47]]]
- 20 B. D. Lucas and T. Kanade, "An iterative image registration technique with an application to stereo vision," in Proceedings of the 7th International Joint Conference on Artificial Intelligence (IJCAI), Vancouver, Canada, 1981, pp. 674-679. https://hal.science/hal-03697340/custom:[[[-]]]
- 21 V . Sarode, X. Li, H. Goforth, Y . Aoki, R. A. Srivatsan, S. Lucey, and H. Choset, "PCRNet: point cloud registration network using PointNet encoding," 2019 (Online). Available: https://arxiv.org/abs/1908.07906.doi:[[[https://arxiv.org/abs/1908.07906]]]
- 22 K. Fu, S. Liu, X. Luo, and M. Wang, "Robust point cloud registration framework based on deep graph matching," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 45, no. 5, pp. 6183-6195, 2023. https://doi.org/10.1109/TPAMI.2022.3204713doi:[[[10.1109/TPAMI.2022.313]]]
- 23 H. Xu, S. Liu, G. Wang, G. Liu, and B. Zeng, "OMNet: learning overlapping mask for partial-to-partial point cloud registration," in Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021, pp. 3112-3121. https://doi.org/10.1109/ICCV48922.2021.00312doi:[[[10.1109/ICCV48922.2021.00312]]]
- 24 Z. Wu, S. Song, A. Khosla, F. Yu, L. Zhang, X. Tang, and J. Xiao, "3D ShapeNets: a deep representation for volumetric shapes," in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 2015, pp. 1912-1920. https://doi.org/10.1109/CVPR.2015.7298801doi:[[[10.1109/CVPR.2015.7298801]]]
- 25 Q. Y . Zhou, J. Park, and V . Koltun, "Open3D: a modern library for 3D data processing," 2018 (Online). Available: https://arxiv.org/abs/1801.09847.doi:[[[https://arxiv.org/abs/1801.09847]]]
- 26 R. B. Rusu and S. Cousins, "3D is here: point cloud library (PCL)," in Proceedings of 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 2011, pp. 1-4. https://doi.org/10.11 09/ICRA.2011.5980567doi:[[[10.11 09/ICRA.2011.5980567]]]
- 27 B. Curless and M. Levoy, "A volumetric method for building complex models from range images," in Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 1996, pp. 303-312. https://doi.org/10.1145/237170.237269doi:[[[10.1145/237170.237269]]]