Ke Xu , Ke Wu and Rongpei Zhou
Probability Weighting Effect in Vertex Cover of Networks Via Prospect-Theoretic Learning
Abstract: Game-theoretic learning methods for the vertex cover problem have been investigated in this paper. In the traditional game theory, the establishment of the game model is based on the complete objectivity of the players, and the existing game models describe the vertex cover problem mainly along this path. In contrast, this paper considers the impact of players’ subjectivity on decision-making results. First, we present a covering game model, where the utility function of the player is established under the prospect theory. Then, by presenting a rounding function, the states of all vertices under Nash equilibrium satisfies vertex cover state of a general network. After then, we present a fictitious play distributed algorithm, which can guarantee that the states of all vertices converge a Nash equilibrium. Finally, the simulation results are presented to assess the impact of players’ subjectivity on the overall cover results of networks.
Keywords: Nash equilibrium , prospect theory , simulation results , subjectivity of players , vertex cover
1. Introduction
Over the past decades, vertex cover (VC) of networks has attracted significant attention due to the wide applications in various fields, such as the wireless sensor networks [1], autonomous intelligent systems [2], target tracking [3], and security surveillance in social networks [4], etc.
To seek the minimum vertex cover of a network, vari- ous distributed optimization algorithms have been proposed, mainly from the perspective of the game-based distributed algorithms, where each vertex is regarded as a player. For example, Yang et al. first used a snowdrift game to describe the vertex cover problem, and presented a memory-based best response distributed algorithm, which can guarantee to obtain a strict Nash equilibrium (SNE) [5]. After then, Tang et al. studied a variant of the vertex cover problem, that is, the weighted vertex cover (WVC) problem, and modeled the problem as an asymmetric game model, and proposed a feedback-based best response algorithm, and obtained a SNE [6]. Recently, Sun et al. formulated the problem as a potential game, and proposed a relaxed greedy and memory-based algorithm, which can also guarantee to obtain a SNE [7]. Other game-based distribute algorithm for solving the (weighted) vertex cover problem include game-based memetic distribute algorithm [8], and time-variant binary log-linear learning al- gorithm [9], etc.
To sum up, the works in [5]-[8] studied the (weighted) ver- tex cover problem from game theoretic perspective. A common assumption is that all players in the game are completely ratio- nal and make appropriate strategies as long as their objective expected functions can be optimized, this assumption is based on expected utility theory. However, numerous experimental studies shown that this assumption deviates from real-life decision-making, and the classical game theory fails to explain the deviations due to player’s subjectivity [10], [11], such as the well-famous Allais’s paradox [12]. For instance, there are two options with A: to win 2500 dollars with probability 0.33 or 2400 dollars with probability 0.66 or nothing with probability 0.01; and B: to win 2400 dollars with probability 1. The experimental results have shown that most players would choose A. But, according to expected utility theory, a preference of B over A implies the B leads to a higher expected utility.
In sum, the subjectivity of players cannot be neglected in the process of decision-making about a particular issue. The vertex cover of social networks is an example of the players involved issues. Thus, for the vertex cover problem, it is very meaningful to consider the players’ subjectivity on the game results. In order to explain the subjectivity of the players in decision results, the prospect theory has been proposed by Kahneman and Tversky [12], which won the 2002 Nobel prize in economic sciences. In recent years, the prospect theory has been widely applied in many fields. For instance, smart grid [13]–[15], requirements management [16], real-life decisions [17], hardware trojan detection [18], vaccination [19], privacy- preserving mechanism [20], quality of experience [21], and data envelopment analysis [22], etc.
In this paper, we considers the impact of players’ subjectiv- ity on decision-making results. For this, we formulated play- ers’ utility (cost) functions based on the prospect theory. By presenting a rounding function, and the vertices’ state under Nash equilibrium satisfies the vertex cover state of network. Moreover, we present a game-based distributed algorithm, i.e., the fictitious play algorithm, and a Nash equilibrium can be obtained.
The main contributions of this paper are summarized as follows.
Table 1.
| Notations | Definitions |
|---|---|
| V | The set of all players (vertices) |
| X | The finite strategy space |
| [TeX:] $$X_i$$ | The strategy set of player [TeX:] $$i$$ |
| μ | The penalty coefficient of uncovered edge |
| [TeX:] $$\omega(\cdot)$$ | The probability weight function |
| a | The rational coefficient |
| [TeX:] $$\Gamma_i$$ | The neighbor set of player [TeX:] $$i$$ |
| T | The superscript for transpose |
| EUT | The expected utility theory |
| PT | The prospect theory |
| [TeX:] $$p_{i, 1}$$ | The probability of choosing strategy 1 for [TeX:] $$i$$ |
| [TeX:] $$p_{i, 0}$$ | The probability of choosing strategy 0 for [TeX:] $$i$$ |
| [TeX:] $$k_i$$ | The degree of player [TeX:] $$i$$ |
| < k > | The average degree of network |
i) We present the player’ utility (cost) function based on prospect theory, and describe the vertex cover problem as a covering game model. Then, we further present a game-based distributed algorithm, i.e, the fictitious play algorithm, which can guarantee to obtain a Nash equilibrium, and it satisfies the vertex cover state of a network.
ii) The simulation results illustrate that deviation from objectivity can strongly impact the overall cover level of networks. Specifically, the more serious the deviation from objectivity, the worse the cover level, and the slower the convergence rate of the fictitious play algorithm.
The paper is organized as follows. In Section II, we introduce prospect theory and formulate a covering game model. In Section III, we explore the relationship between the vertex cover and Nash equilibrium of the formulated game model. In Section IV, we present a fictitious play distributed algorithm, and prove that the states of all vertices converge to a Nash equilibrium. In Section V, numerical simulation results are presented to demonstrate the effectiveness of the presented algorithm, and show the impact of subjectivity on cover results. Finally, conclusions of this paper are drawn in Section VI. Note that the notations used in this paper are listed in Table I.
II. PRELIMINARIES AND PROBLEM FORMULATION
A. Prospect Theory
Expected utility theory (EUT) allows each player to evaluate an objective expected utility, and then makes corresponding decision. However, in the real-life scenarios, players’ behavior will deviate from the rational behavior predicted by the EUT. This phenomenon is attributed to the risk and uncertainty that players often face when making decisions.
Fortunately, the prospect theory (PT) can be used to model how players behave irrationally under the risk and uncertainty circumstances [12]. An important concept of the PT is proba- bility weight effect, which converts objective probability into subjective probability, so as to establish a prospect game model of players. For probability weight effect, it reveals that each player [TeX:] $$i$$ adopts his subjective probability [TeX:] $$w_i\left(p_i\right)$$ rather than objective probability [TeX:] $$p_i$$, where subjective probability [TeX:] $$w_i\left(p_i\right)$$ is a nonlinear transformation from [TeX:] $$p_i$$ to [TeX:] $$w_i\left(p_i\right)$$ [23]–[25]. Without loss of generality, we can assume that [TeX:] $$w_i\left(p_i\right)$$) is the same for all players, i.e., [TeX:] $$w_i\left(p_i\right)$$ = [TeX:] $$w\left(p_i\right)$$. At present, the Prelec function is widely used as a classical weight function [26], which is described as
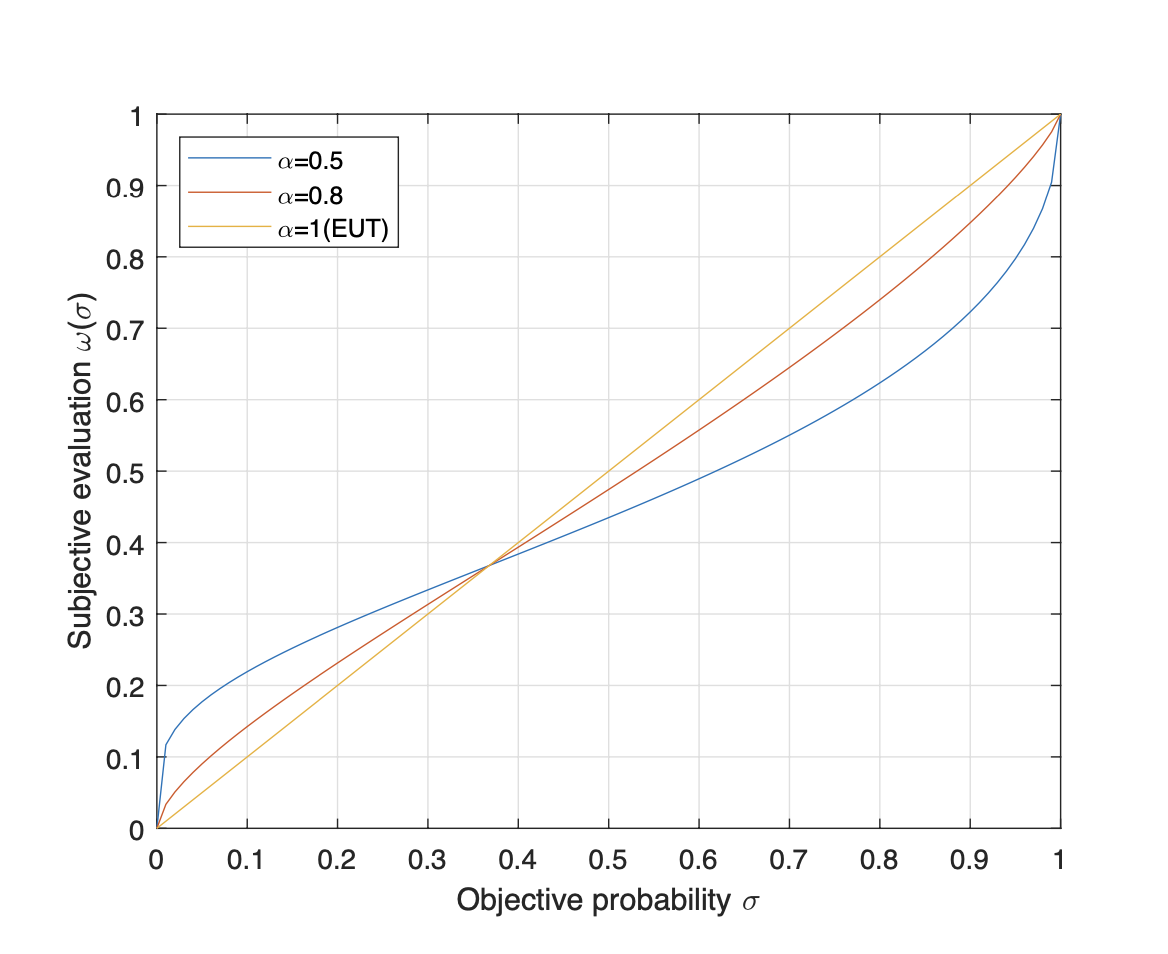
where [TeX:] $$\sigma$$ and [TeX:] $$\omega(\sigma)$$ are the objective and subjective probability, respectively; α ∈ (0,1] is a rational coefficient, which reveals how a player subjective evaluation distorts the objective probability. The greater the rational coefficient α, the higher the rational degree. It is worth noting that when α = 1, the probability weight effect will coincide with the probability of the EUT. An illustration on the impact of α is shown in Fig. 1.
From Fig. 1, we can observe that the probability weight function [TeX:] $$\omega(\sigma)$$ has some properties, include: i) It is asymmetric with fixed point and inflection point at (1/e,1/e); ii) When 0 < σ < 1/e, ω(σ) > σ, moreover, 1/e < σ < 1, ω(σ) < σ; iii) ω(0) = 0, ω(1) = 1; iv) It is concave if 0 < σ ≤ 1/e and convex if 1/e < σ ≤ 1; v) A small α results in a more curved probability weight function.
B. Game Model
An undirected graph is defined by [TeX:] $$\Xi$$ = {V,E}, where V = {1,···,n} is the set of vertices and E = {[TeX:] $$e_{i j}$$} is the set of edges. For an undirected graph [TeX:] $$\Xi$$, [TeX:] $$e_{i j}$$ = 1 if an edge exists between vertex i and vertex j; otherwise, [TeX:] $$e_{i j}$$ = 0. A subset VVC of V is called a vertex cover if, for each edge [TeX:] $$e_{i j}\left(e_{i j} \in E\right)$$ has at least one endpoint (vertex) belongs to [TeX:] $$V_{\mathrm{VC}}$$. A minimum vertex cover [TeX:] $$V_{\mathrm{MVC}}$$ is a vertex cover [TeX:] $$V_{\mathrm{VC}}$$ with the minimum cardinality.
The vertex cover problem can be formulated as a covering game, denoted by [TeX:] $$G=\left\{V,\left\{X_i\right\}_{i \in V},\left\{u_i\right\}_{i \in V}, E\right\}$$ , where [TeX:] $$X_i$$ = {0, 1} (0 and 1 are the uncovered and covered strategies, respectively) is the strategy set of player (vertex) [TeX:] $$i, \forall i \in V$$ strategy profile of all players is [TeX:] $$x=\left(x_1, \cdots, x_n\right) \in X$, $x_i \in X_i$$; and [TeX:] $$u_i$$ is the utility (cost) function of player [TeX:] $$i$$ [5].
Based on the above definition, the cost function for a player [TeX:] $$i(i \in V)$$ is given by [27], [28] where [TeX:] $$x_{-i}=\left(x_1, \cdots, x_{i-1}, x_{i+1}, \cdots, x_n\right)$$ is the strategy profile of all players except player [TeX:] $$i$$; The first item on the right of (2) represents the cost that player [TeX:] $$i$$ pays if he chooses the covered strategy. μ > 0 is penalty coefficient, the corresponding second item represents the penalty of an uncovered edge.
(2)
[TeX:] $$u_i\left(x_i, x_{-i}\right)=x_i+\mu\left(1-x_i\right) \sum_{j=1}^n\left(1-x_j\right) e_{i j}$$In the covering game G, we will model the player’s cost function based on the continuous strategies, rather than discrete and deterministic strategies. Intuitively, continuous strategy [TeX:] $$p_{i, x_i} \in[0,1]$$ in this paper is a probabilistic choice, which captures the frequency of players choosing the strategy [TeX:] $$x_i$$. In this case, let [TeX:] $$p=\left(p_{1,1}, \cdots, p_{n, 1}\right)$$ be the continuous strategy profile of all players, which is a row vector.
In the EUT, each player can objectively evaluate each neigh- bor’s probabilistic choice, and objectively select his continuous strategy [TeX:] $$p_{i, x_i} \in[0,1]$$ to optimize his cost. Thus, the cost of player [TeX:] $$i$$ under the EUT is given by
(3)
[TeX:] $$\begin{aligned} U_i^{\mathrm{EUT}}(p) & =U_i^{\mathrm{EUT}}\left(p_{i, 1}, p_{-i, 1}\right) \\ & =p_{i, 1}+\mu\left(1-p_{i, 1}\right) \sum_{j=1}^n\left(1-p_{j, 1}\right) e_{i j} \end{aligned}$$where [TeX:] $$p_{i, 1}$$ is the probability of choosing covered strategy 1 for player [TeX:] $$i ; p_{-i, 1}=\left[p_{1,1}, \cdots, p_{i-1,1}, p_{i+1,1}, \cdots, p_{n, 1}\right]$$ is the continuous strategy profile of all players other than player [TeX:] $$i$$.
In this paper, we consider applying the probability weight effect of prospect theory for modeling, that is, each player will subjectively evaluate the neighbor’s continuous strategy. Thus, the cost of player [TeX:] $$i$$ under the PT is given by
(4)
[TeX:] $$\begin{aligned} U_i^{\mathrm{PT}}(p) & =U_i^{\mathrm{PT}}\left(p_{i, 1}, p_{-i, 1}\right) \\ & =p_{i, 1}+\mu\left(1-p_{i, 1}\right) \sum_{j=1}^n\left(1-\omega_i\left(p_{j, 1}\right)\right) e_{i j} \end{aligned}$$where [TeX:] $$\omega_i(\cdot)$$ is the Prelec function, which is shown in (1).
For each player [TeX:] $$i$$, he plays the covering game by solving the following optimization problem as
where [TeX:] $$U_i(\cdot)$$ can be either the EUT cost (3) or the PT cost (4).
III. RELATIONSHIP BETWEEN VC AND NE OF GAME MODEL
Definition 1 : A Nash equilibrium [TeX:] $$p^*=\left(p_{1,1}^*, \cdots, p_{n, 1}^*\right)$$ is such the continuous strategy profile where no player can decrease his cost by changing his continuous strategy [29], i.e.,
(6)
[TeX:] $$U_i\left(p_{i, 1}^*, p_{-i, 1}\right) \leq U_i\left(p_{i, 1}^{\prime}, p_{-i, 1}\right)$$where [TeX:] $$\forall p_{i, 1}^{\prime} \neq p_{i, 1}^*$$. Note that the Nash equilibrium (NE) defined in (6) is applicable for both the EUT and the PT, the difference would be in whether one is using (3) or (4), respectively.
Note that for any continuous strategic game, there exists at least one NE under both the EUT and the PT. Define [TeX:] $$p^{\mathrm{EUT}}=\left(p_{1,1}^{\mathrm{EUT}}, \cdots, p_{n, 1}^{\mathrm{EUT}}\right) \text { and } p^{\mathrm{PT}}=\left(p_{1,1}^{\mathrm{PT}}, \cdots, p_{n, 1}^{\mathrm{PT}}\right)$$ be a 1,1 n,1 1,1 n,1 NE of the EUT and the PT, respectively. Next, I give an example to illustrate it.
Example 1: Consider three players to perform covering game, penalty coefficient μ is set to 1.6, adjacency matrix is
it is easy to check that there exists seven NEs regardless of the [TeX:] $$\alpha$$. For instance, if rational coefficient [TeX:] $$\alpha$$ = 1, and seven NEs are [TeX:] $$p^{\mathrm{EUT}, 1}$$ = (0, 1, 1), [TeX:] $$p^{\mathrm{EUT}, 2}$$ = (1, 0, 1), [TeX:] $$p^{\mathrm{EUT}, 3}$$ = (1, 1, 0), [TeX:] $$p^{\mathrm{EUT}, 4}$$ = (1, 0.375, 0.375), [TeX:] $$p^{\mathrm{EUT}, 5}$$ = (0.375,1,0.375), [TeX:] $$p^{\mathrm{EUT}, 6}$$ = (0.375,0.375,1), and [TeX:] $$p^{\mathrm{EUT}, 7}$$ = (0.6875, 0.6875, 0.6875).
Proposition 1: Consider a covering game G, if penalty coefficient μ > e/(e − 1), any NE [TeX:] $$p^*=\left(p_{i, 1}^*, \cdots, p_{n, 1}^*\right)$$ under both the EUT and the PT satisfies: if [TeX:] $$p_{i, 1}^* \leq 1 / e$$, then [TeX:] $$\forall j \in \Gamma_i, p_{i 1}^*>1 / e$$. Note that the NE [TeX:] $$p^*$$ can be either the EUT or the PT.
Proof: Suppose that [TeX:] $$\exists j^{\prime} \in \Gamma_i$$, such that [TeX:] $$p_{j^{\prime}, 1}^* \leq 1 / e$$. Let [TeX:] $$p_{i, 1}^{\prime}>1 / e$$.
Under the EUT, according to Definition 1, the following inequation
(7)
[TeX:] $$\begin{aligned} U_i^{\mathrm{EUT}} & \left(p_{i, 1}^*, p_{-i, 1}^*\right)-U_i^{\mathrm{EUT}}\left(p_{i, 1}^{\prime}, p_{-i, 1}^*\right) \\ & =\left(p_{i, 1}^*-p_{i, 1}^{\prime}\right)\left(1-\mu \sum_{j=1}^n\left(1-p_{j, 1}^*\right) e_{i j}\right) \leq 0 \end{aligned}$$holds
Since [TeX:] $$p_{i, 1}^*-p_{i, 1}^{\prime}$$ < 0, and
then
which is a contradiction to (7). Thus, the hypothesis is not hold.
Under the PT, according to Definition 1, the following inequation
(8)
[TeX:] $$\begin{aligned} & U_i^{\mathrm{PT}}\left(p_{i, 1}^*, p_{-i, 1}^*\right)-U_i^{\mathrm{PT}}\left(p_{i, 1}^{\prime}, p_{-i, 1}^*\right) \\ & \quad=\left(p_{i, 1}^*-p_{i, 1}^{\prime}\right)\left(1-\mu \sum_{j=1}^n\left(1-\omega_i\left(p_{j, 1}^*\right)\right) e_{i j}\right) \leq 0 \end{aligned}$$holds.
Since
then
which is a contradiction to (8). Thus, the hypothesis is not hold. Hence, the proof is completed.
Further, we define a rounding function
(9)
[TeX:] $$s_i\left(p_{i, 1}\right)= \begin{cases}0, & p_{i, 1} \leq 1 / e \\ 1, & p_{i, 1}>1 / e\end{cases}$$if [TeX:] $$s_i\left(p_{i, 1}\right)$$ = 1, we consider that the state of player [TeX:] $$i$$ is a i i,1 covered state; otherwise, it is an uncovered state. Besides, define s = [TeX:] $$\left(s_1, \cdots, s_n\right)$$ be the state profile for all players, where [TeX:] $$s_i=s_i\left(p_{i, 1}\right)$$.
According to (9), a theorem is given as follows
Theorem 1: Consider a covering game G, if penalty coeffi- cient μ > e/(e − 1), any NE [TeX:] $$p^*$$ satisfies: if [TeX:] $$s_i\left(p_{i, 1}^*\right)$$ = 0, then [TeX:] $$\forall j \in \Gamma_i, s_j\left(p_{j, 1}^*\right)$$ = 1, where [TeX:] $$\Gamma_i$$ is the neighbor set of [TeX:] $$i$$.
Remark 1: The Theorem 1 shows that there no 0-0 edge (uncover edge) under certain constraint of penalty coefficient μ. In this case, the vertices’ state under any NE under Nash equilibrium satisfies vertex cover state of a general network. This relationship is only determined by the game model other than any network topology or any algorithm.
IV. OPTIMIZATION APPROACH-FICTITIOUS PLAY AND CONVERGENCE ANALYSIS
A. Fictitious Play Algorithm
In this subsection, we present a fictitious play distributed algorithm, which requires the minimum memory length 1, that is, each player only need his previous strategy (the probability t of choosing strategy 1. The algorithm is raised from the fictitious play (FP) [30]. Although there exist many distributed algorithms can find a NE [31]–[33], the FP distributed algo- rithm is well-known as a popular algorithm for players, which is a simple and practical algorithm that can keep an acceptable running time [34]. We present the FP distributed algorithm as follows and the pseudo-code in Table II.
At each time step [TeX:] $$t$$, the probability [TeX:] $$p_{i, 1}^t$$ of player [TeX:] $$i$$ is updated as
where [TeX:] $$p_{i, 1}^t$$ is the probability of player [TeX:] $$i$$ choosing strategy 1 at time step [TeX:] $$t$$, and [TeX:] $$v_{i, 1}^t$$ is determined by
(11)
[TeX:] $$v_{i, 1}^t= \begin{cases}1, & \text { if } \underset{x_i \in\{0,1\}}{\arg \min } U_i\left(x_i, p_{-i, 1}^{t-1}\right)=1 \\ 0, & \text { otherwise }\end{cases}$$where the [TeX:] $$U_i\left(x_i, p_{-i, 1}^{t-1}\right)$$ is the cost obtained by player [TeX:] $$i$$ with re- spect to the continuous strategy profile of the neighbors, when player [TeX:] $$i$$ chooses strategy [TeX:] $$x_i$$ at time step [TeX:] $$t$$. Besides, the cost [TeX:] $$U_i\left(x_i, p_{-i, 1}\right)$$ can be either cost of the EUT [TeX:] $$U_i^{\mathrm{EUT}}\left(x_i, p_{-i, 1}^{t-1}\right)$$ or cost of the PT [TeX:] $$U_i^{\mathrm{PT}}\left(x_i, p_{-i, 1}^{t-1}\right)$$.
The stopping criterion of the presented algorithm can be defined as
where [TeX:] $$Q$$ is an arbitrary large number (typically goes to tttT infinity), [TeX:] $$P_i^t=\left[p_{i, 1}^t, p_{i, 0}^t\right]^T$$.
B. Convergence Analysis
The presented algorithm can guarantee that any continuous strategy profile converges to an equilibrium state after a certain time steps [35]. Given any continuous strategy profile, suppose
Table II.
| Algorithm 1: Fictitious play algorithm |
|---|
| Input: Undirected network [TeX:] $$\Xi$$; penalty coefficient [TeX:] $$\mu$$; rational coefficient [TeX:] $$a$$; initial continuous strategy profile [TeX:] $$p^0$$. Output: NE [TeX:] $$p^*$$; state profile [TeX:] $$s^*$$. repeat: Each player [TeX:] $$i$$ obtains neighbors’ continuous strategy profile\ at time [TeX:] $$t$$: [TeX:] $$p_{-i, 1}^{t-1}$$Calculate cost of each discrete strategy by (3), (4): [TeX:] $$U_i^{\mathrm{EUT}}\left(x_i, p_{-i, 1}^{t-1}\right), U_i^{\mathrm{PT}}\left(x_i, p_{-i, 1}^{t-1}\right), \forall x_i \in X_i$$ Update the value [TeX:] $$v_{i, 1}^t, \forall i \in V$$ by (11);\ Each player [TeX:] $$i$$ updates the probability of playing strategy 1 by (10): [TeX:] $$p_{i, 1}^t=\left(1-\frac{1}{t}\right) p_{i, 1}^{t-1}+\frac{1}{t} v_{i, 1}^t$$Until: Convergence to a stopping criterion by (12): [TeX:] $$\max \left|P_i^t-P_i^{t-1}\right| \leq \frac{1}{Q}$$ |
it converges to an equilibrium state [TeX:] $$p^*=\left(p_{i, 1}^*, \cdots, p_{n, 1}^*\right)$$ after [TeX:] $$t^*$$ time steps. Then for [TeX:] $$t>t^*$$, the [TeX:] $$P_i^t$$ follows that
where [TeX:] $$\epsilon$$ < 1 is a positive constant.
The following Theorem proves that the equilibrium state is a NE under both the EUT and the PT.
Theorem 2: Consider a covering game G, the presented algorithm in (10) can guarantee that any continuous strategy profile converges to a NE under both the EUT and the PT.
proof : According to (3) and (4), we have
(14)
[TeX:] $$U_i\left(p_{i, 1}, p_{-i, 1}\right)=p_{i, 1} U_i\left(1, p_{-i, 1}\right)+\left(1-p_{i, 1}\right) U_i\left(0, p_{-i, 1}\right)$$where [TeX:] $$U_i$$(·) can be either the EUT cost or the PT cost.
Define {[TeX:] $$p^t$$} is the presented algorithm process. For the EUT, we can suppose that {[TeX:] $$p^t$$} will converge to an equilibrium state [TeX:] $$p^{\prime}=\left(p_{i, 1}^{\prime}, p_{-i, 1}^{\prime}\right)$$ after time step [TeX:] $$t^{\prime}$$. So, [TeX:] $$v_{i .1}^{t^{\prime}}=v_{i .1}^{t^{\prime}+\beta}, \forall \beta>0$$. I assume that the p is not NE, according to Definition 1, there must exist one player [TeX:] $$i$$ can decrease his cost by changing his continuous strategy.
i) If [TeX:] $$p_{i, 1}^{\prime}$$ = 1, then there exist a [TeX:] $$p_{i, 1} \neq p_{i, 1}^{\prime}$$ such that
According to (14), we have
it implies
(15)
[TeX:] $$U_i^{\mathrm{EUT}}\left(1, p_{-i, 1}^{\prime}\right)>U_i^{\mathrm{EUT}}\left(0, p_{-i, 1}^{\prime}\right),$$thus, for β > 0, we have [TeX:] $$v_{i, 1}^{t^{\prime}} \neq v_{i, 1}^{t^{\prime}+\beta}$$. ii) If [TeX:] $$p_{i, 1}^{\prime}$$ = 0, similarly, then there exist a [TeX:] $$p_{i, 1} \neq p_{i, 1}^{\prime}$$ such that
(16)
[TeX:] $$U_i^{\mathrm{EUT}}\left(1, p_{-i, 1}^{\prime}\right)<U_i^{\mathrm{EUT}}\left(0, p_{-i, 1}^{\prime}\right)$$then, for β > 0, we have [TeX:] $$v_{i, 1}^{t^{\prime}} \neq v_{i, 1}^{t^{\prime}+\beta}$$.
Fig. 2.
iii) If [TeX:] $$p_{i, 1}^{\prime} \in(0,1)$$, there exist [TeX:] $$x_i, x_i^{\prime} \in X_i, x_i \neq x_i^{\prime}$$, such that
(17)
[TeX:] $$U_i^{\mathrm{EUT}}\left(x_i, p_{-i, 1}^{\prime}\right)<U_i^{\mathrm{EUT}}\left(x_i^{\prime}, p_{-i, 1}^{\prime}\right)$$where [TeX:] $$p_{i, x_i^{\prime}}$$ > 0. Thus, we can choose a value [TeX:] $$\epsilon$$ that satisfies
(18)
[TeX:] $$0<\epsilon<\frac{1}{2}\left|U_i^{\mathrm{EUT}}\left(x_i^{\prime}, p_{-i, 1}^{\prime}\right)-U_i^{\mathrm{EUT}}\left(x_i, p_{-i, 1}^{\prime}\right)\right|$$as [TeX:] $$p^t$$ converges to [TeX:] $$p^{\prime}$$ at time step [TeX:] $$t^{\prime}$$.
Since the presented algorithm process decreases as the number of time steps, the cost distance of a discrete strategy between two neighboring iterations must be less than ε after a certain time steps [TeX:] $$t^{\prime}$$. For t ≥ [TeX:] $$t^{\prime}$$, we have
(19)
[TeX:] $$U_i^{\mathrm{EUT}}\left(x_i, p_{-i, 1}^t\right)-U_i^{\mathrm{EUT}}\left(x_i, p_{-i, 1}^{\prime}\right) \leq \epsilon$$
(20)
[TeX:] $$U_i^{\mathrm{EUT}}\left(x_i^{\prime}, p_{-i, 1}^{\prime}\right)-U_i^{\mathrm{EUT}}\left(x_i^{\prime}, p_{-i, 1}^t\right) \leq \epsilon$$Thus, for t ≥ [TeX:] $$t^{\prime}$$, the presented algorithm process can be written as
(21)
[TeX:] $$\begin{aligned} U_i^{\mathrm{EUT}}\left(x_i^{\prime}, p_{-i, 1}^t\right) & \geq U_i^{\mathrm{EUT}}\left(x_i^{\prime}, p_{-i, 1}^{\prime}\right)-\epsilon \\ & >U_i^{\mathrm{EUT}}\left(x_i, p_{-i, 1}^{\prime}\right)+\epsilon \\ & \geq U_i^{\mathrm{EUT}}\left(x_i, p_{-i, 1}^t\right) \end{aligned}$$thus, player [TeX:] $$i$$ would not choose the strategy [TeX:] $$x_i^{\prime}$$ but would rather choose strategy [TeX:] $$x_i$$ after [TeX:] $$t^{\prime}$$ time steps. Thus, we have [TeX:] $$p_{i, x_i^{\prime}}$$ = 0. To sum up, the above three cases show that the hypothesis is not hold. Thus the equilibrium state [TeX:] $$p^{\prime}$$ is a NE.
For the PT, since the Prelec function [TeX:] $$w_i$$(·) is continuous and monotonically increasing function over [0,1]. Thus, it is easy to check that an equilibrium state [TeX:] $$p^{\prime \prime}$$ under the PT is also NE. Hence, the proof is completed.
V. SIMULATION EXPERIMENT AND ANALYSIS
In this paper, the simulation on a variety of networks for illustrating how players’ behaviors impact the overall cover level of networks under both the EUT and the PT, where the networks include the ER random networks [36], the WS small- world networks [37], and the BA scale-free networks [38]. To obtain a NE under both the EUT and the PT, we use the presented algorithm. Moreover, the rational coefficient α is set to 0.5, 0.8 and 1, respectively; the [TeX:] $$Q$$ needs to be set to a large value, i.e., 10000; and the initial continuous strategy profile [TeX:] $$p^0$$ is generated randomly to ensure that the simulation results are not affected by the initial settings.
In this subsection, we consider the three categories of networks with size [TeX:] $$n$$ = 1000. For the WS networks, we consider two cases: WS(I) and WS(II), where the probability [TeX:] $$p_w$$ of rewiring each edge is 0.1 and 0.5, respectively. For the BA network, the probability [TeX:] $$p_b$$ that a new node is connected to an existing node [TeX:] $$i$$ is [TeX:] $$k_i / \sum_j k_j$$. Moreover, the average degree < k > of a network is set to 4. For the convenience of comparison, two indicators are introduced as
(23)
[TeX:] $$f(s)=\sum_{i=1}^n\left[s_i+n\left(1-s_i\right) \sum_{j=1}^n\left(1-s_j\right) e_{i j}\right] .$$In (22), f(p) represents the proportion of covered strategy 1 in the network. In (23), the formula’s first part calculates the number of covered vertices of the network, and the second part penalizes any uncovered edge [TeX:] $$e_{i j}$$ (i.e., [TeX:] $$e_{i j}$$ = 0) with the value [TeX:] $$n$$. The smaller the value [TeX:] $$f(s)$$, the fewer vertices are covered in the network. In particular, if there exists at least one uncovered edge of a network, then we have [TeX:] $$f(s)>n$$; otherwise, [TeX:] $$f(s) \leq n$$.
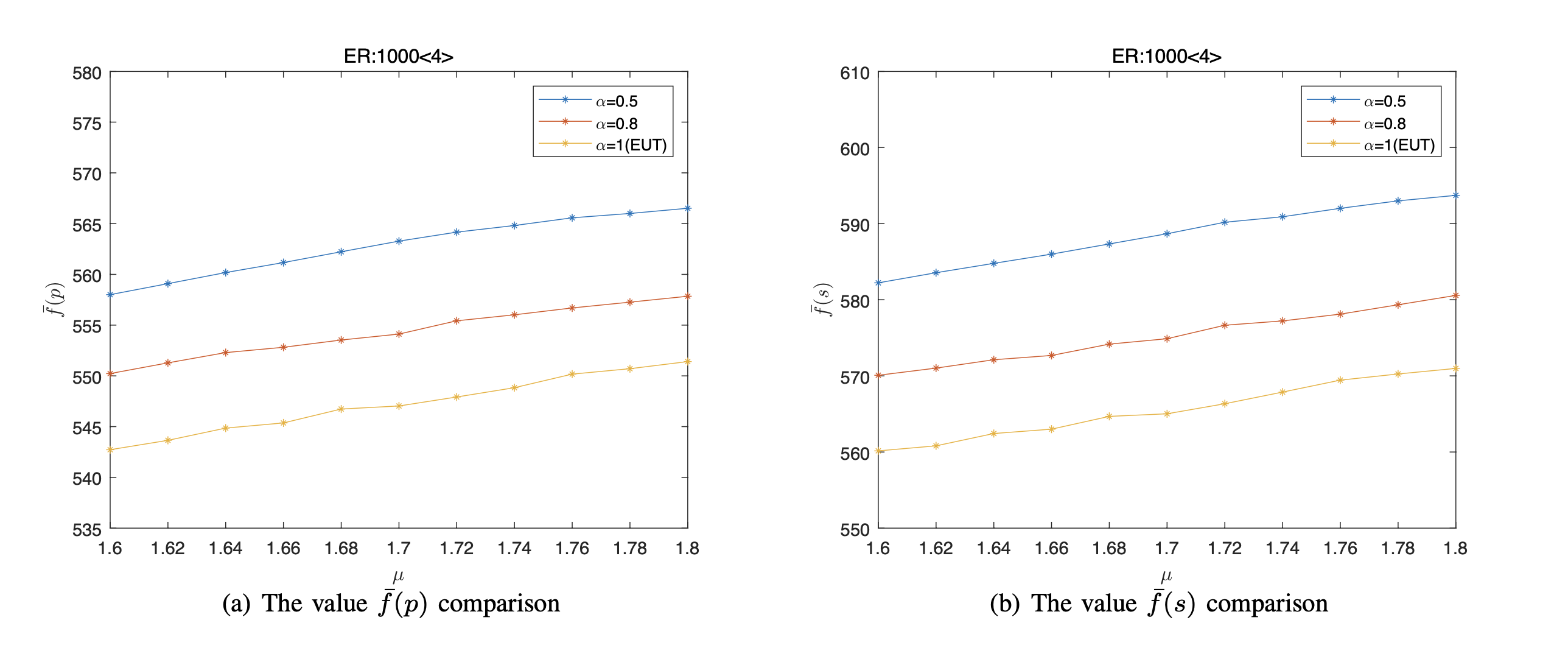
For each μ, we independently repeat 100 runs of the simulations on each network for each datum, and obtained the average value [TeX:] $$\bar{f}(p)$$ and the average value [TeX:] $$\bar{f}(s)$$. The [TeX:] $$\bar{f}(p)$$ and the [TeX:] $$\bar{f}(s)$$ of different values μ on the several networks are shown in Figs. 2–5. Note that the [TeX:] $$\bar{f}(s)$$ is used to reflect thez cover level of networks.
From Figs. 2–5, we can obtain that
i) Since we can always obtain a stable value by running the proposed algorithm at each run, thus there exists at least one NE under both the EUT and the PT on different networks via the presented algorithm. Moreover, for different networks, the NE are different even if n, < k >, and μ are the same.
Fig. 3.
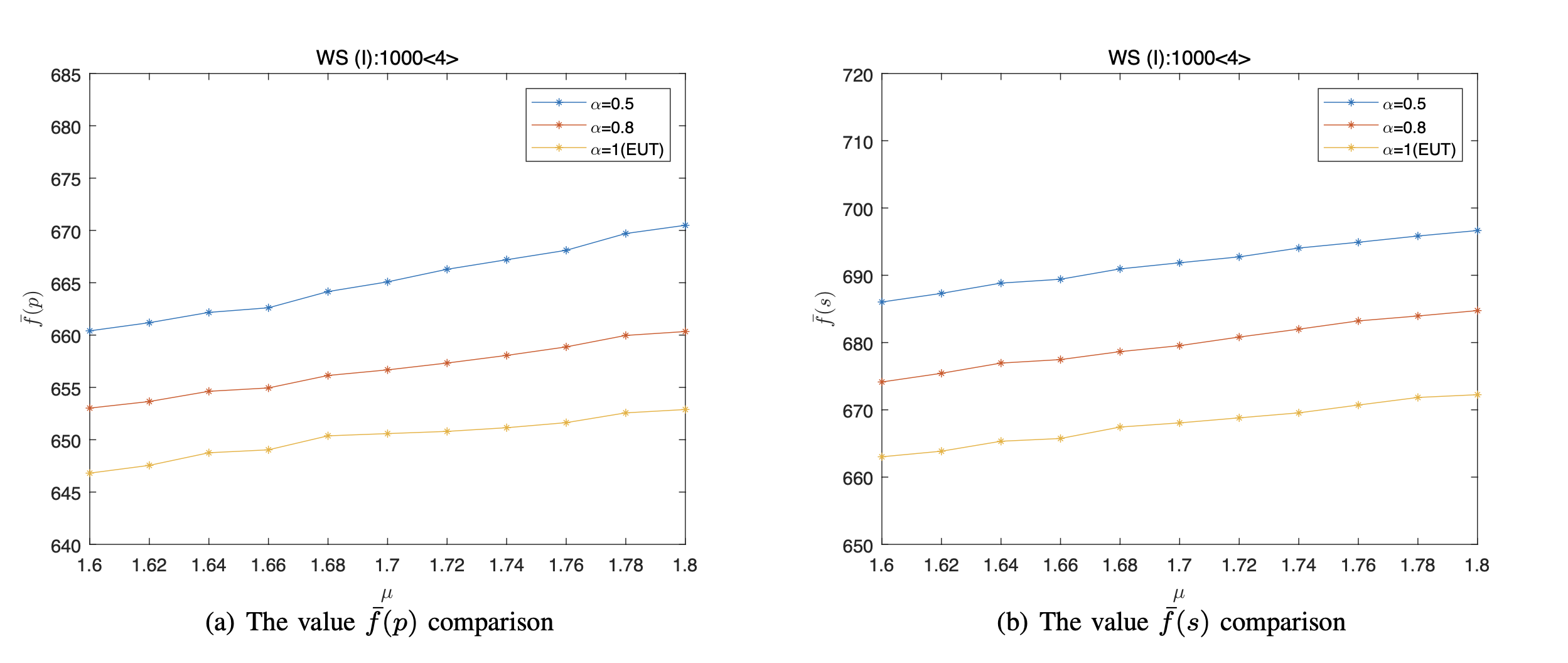
Fig. 4.
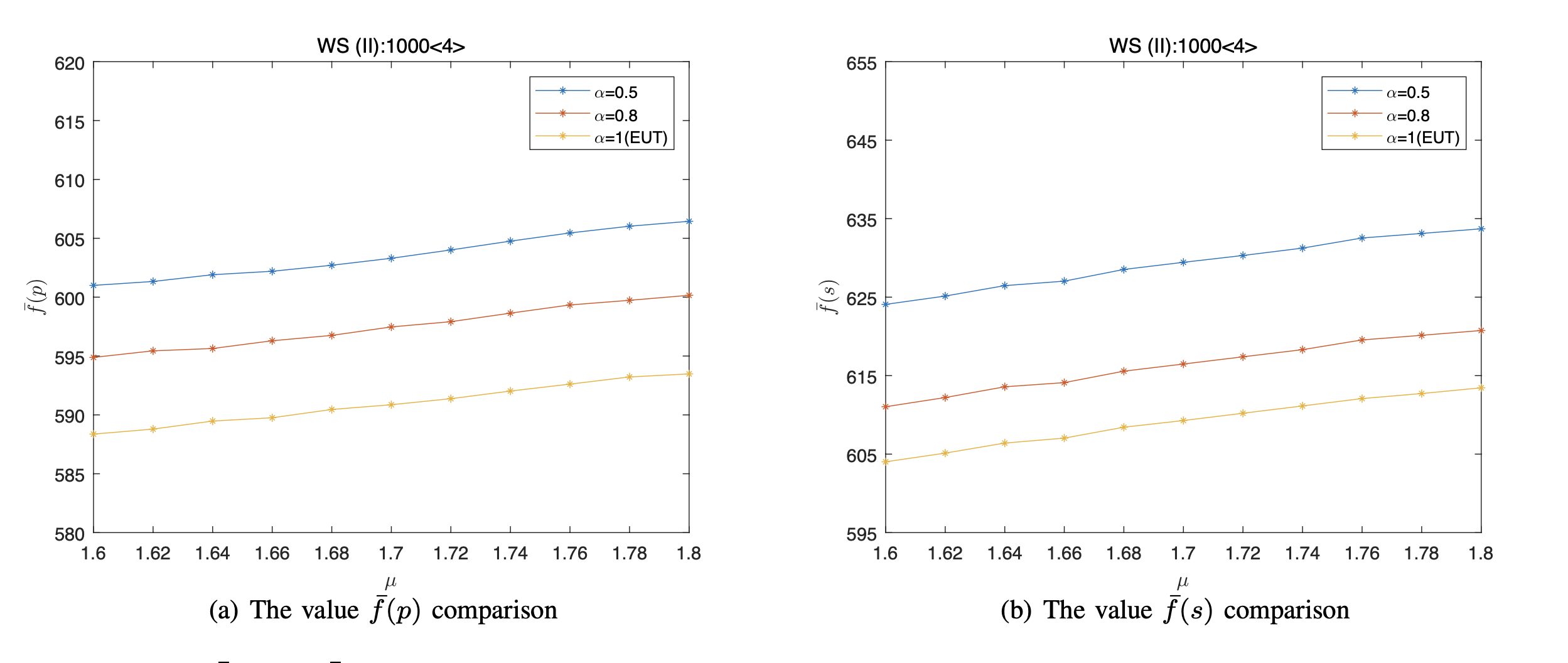
Fig. 5.
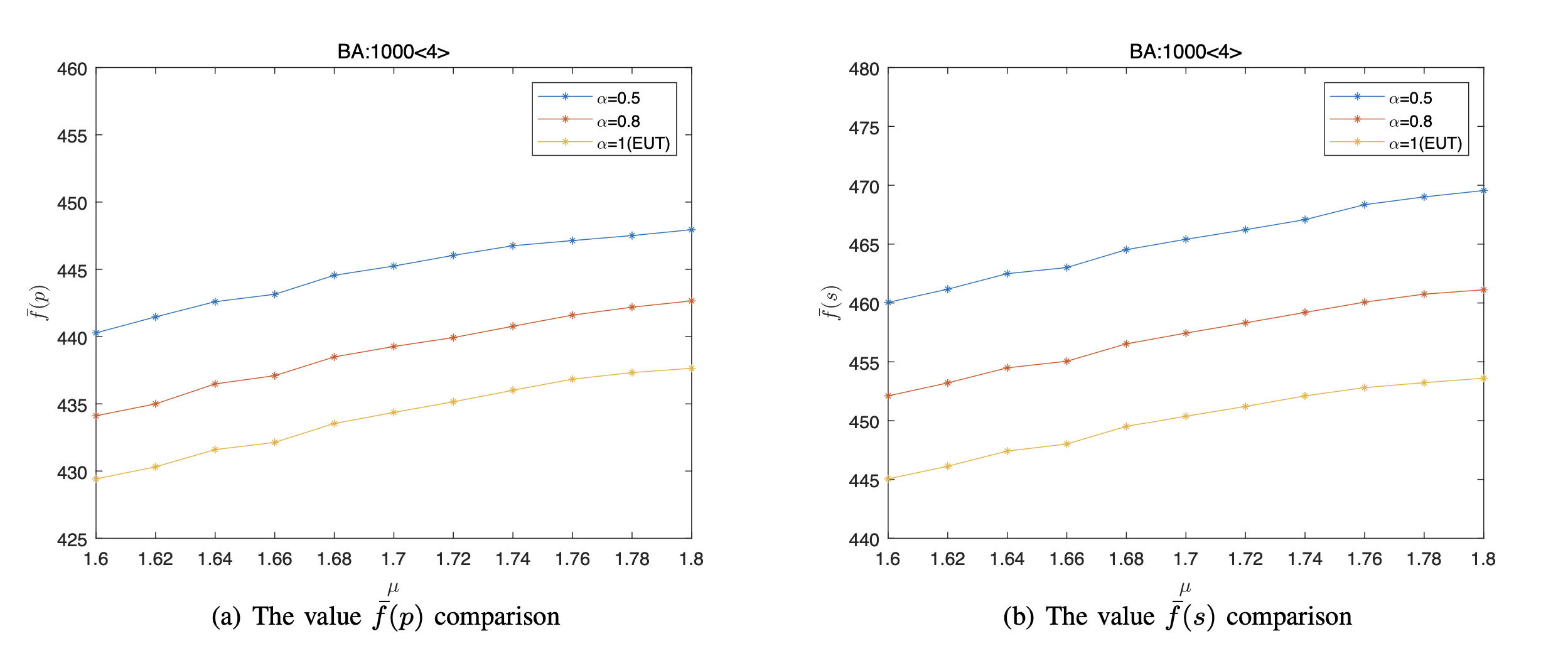
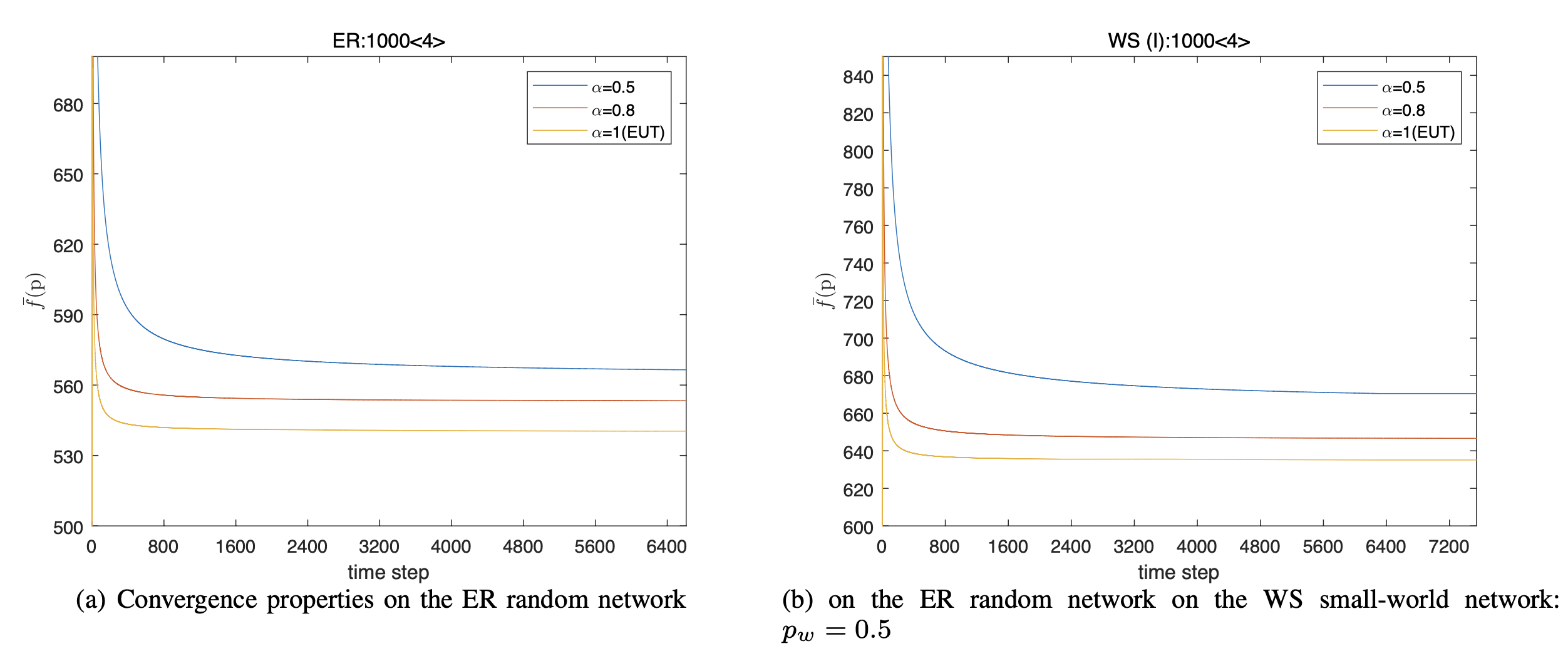
Fig. 6.
ii) Since the value [TeX:] $$\bar{f}(s)$$ is less than [TeX:] $$n$$, thus the vertices’ state under the NE satisfy the vertex cover of network, where the number of covered vertices of the BA network is the least, while that of the WS (I) network is the most.
iii) As penalty coefficient μ increases, the value [TeX:] $$\bar{f}(p)$$ also increases under both the EUT and the PT. For instance, for the ER random network, when we fix α = 0.5 and μ varies from 1.6 to 1.8, the value [TeX:] $$\bar{f}(p)$$ is calculated to grow by 1.65% from 558.01 to 567.21.
iv) More importantly, The NE are different between the PT and the EUT. Compared the EUT, the [TeX:] $$\bar{f}(p)$$ is larger under the PT. More specifically, the smaller the rational coefficient α, the larger the value [TeX:] $$\bar{f}(p)$$. In other words, compared with the EUT, the overall cover probability of the network will increase in which deviate from the rational behavior. Take the WS(I) 1000 < 4 > network for example. Under the PT, when we fixed μ = 1.8, the value [TeX:] $$\bar{f}(p)$$ increases from 652.89 to 659.74 as α varies from 1 to 0.8, and the value [TeX:] $$\bar{f}(p)$$ increases from 659.74 to 675.89 as α varies from 0.8 to 0.5.
v) Moreover, the [TeX:] $$\bar{f}(p)$$ and the [TeX:] $$\bar{f}(s)$$ have the same trend of change, that is, the [TeX:] $$\bar{f}(s)$$ increases as the [TeX:] $$\bar{f}(p)$$ increases.
Finally, we examine the convergence rate with different rational coefficient α. Fig. 6 shows the process of the conver- gence to the equilibrium state on the ER and WS(I) networks under both EUT and PT, respectively, where μ is set to 1.8. Thus, we can see that compared the EUT, the convergence rate of the presented algorithm is slower under the PT. More specifically, the smaller the rational coefficient α, the slower the convergence rate. Here, note that even though the number of time steps required for the players’ strategies to converge is large, the computational requirement of each time step is low. Thus, from our generated results, the convergence time with each α is short. If need, in order to accelerate the convergence rate, a small [TeX:] $$Q$$ is suggested to adopted, but at the expense of obtaining an approximate state rather than an exact NE. In sum, the more serious the deviation from objectivity, the worse the cover level, and the slower the convergence rate of the fictitious play algorithm.
VI. CONCLUSION
In this paper, we have introduced a game-based approach for studying the vertex cover problem, and explicitly considered the subjectivity of players. In particular, we have developed a covering game model based on prospect theory, where each player subjectively observes his neighbors’ strategies, and determines his strategy in order to minimize the cost under the prospect theory. Then, we have presented a fictitious play distributed algorithm and proved that any state reach a NE under both the EUT and the PT. The simulation result have shown that deviations from objective game-theoretic approach can leads to unexpected results, which depends on the subjective degree of the players. That is, players with a high rational degree will help to obtain wonderful cover results of a network. Future work will focus on vertex cover of networks under the framing effect of the prospect theory [39], [40].
Biography
Ke Wu
Ke Wu Ke Wu received her B.S. and M.S. degree both from the School of Mathematics and Information Science, Nanchang Hangkong University. She is currently a Lecturer at the School of Science, Guilin University of Aerospace Technology, also at Basic Department, Jiangxi Manufacturing Polytechnic College. Her research interests include traffic planning, game theory and networked optimization.
Biography
References
- 1 B. Lin, "Research on data release and location monitoring technology of sensor network based on Internet of things," J. Web Eng., pp. 689-712, 2021.doi:[[[10.13052/jwe1540-9589.2036]]]
- 2 J. J. Q. Yu and A. Y . S. Lam, "Autonomous vehicle logistic system: Joint routing and charging strategy," IEEE Trans. Intell. Transp. Syst., vol. 19, no. 7, pp. 2175-2187, 2018.doi:[[[10.1109/tits.2017.2766682]]]
- 3 S. Son, J. Kwon, H.-Y . Kim, and H. Choi, "Tiny drone tracking framework using multiple trackers and kalman-based predictor," J. Web Eng., pp. 2391-2412, 2021.doi:[[[10.13052/jwe1540-9589.2088]]]
- 4 J. Zhou, Z. Cao, X. Dong, N. Xiong, and A. V . Vasilakos, "4s: A secure and privacy-preserving key management scheme for cloudassisted wireless body area network in m-healthcare social networks," Inform. Sci., vol. 314, pp. 255-276, 2015.doi:[[[10.1016/j.ins.2014.09.003]]]
- 5 Y . Yang and X. Li, "Towards a snowdrift game optimization to vertex cover of networks," IEEE Trans. Cybern., vol. 43, no. 3, pp. 948-956, 2013.doi:[[[10.1109/tsmcb.2012.2218805]]]
- 6 C. Tang, A. Li, and X. Li, "Asymmetric game: A silver bullet to weighted vertex cover of networks," IEEE Trans. Cybern., vol. 48, no. 10, pp. 2994-3005, 2018.doi:[[[10.1109/tcyb.2017.2754919]]]
- 7 C. Sun, W. Sun, X. Wang, and Q. Zhou, "Potential game theoretic learning for the minimal weighted vertex cover in distributed networking systems," IEEE Trans. Cybern., vol. 49, no. 5, pp. 1968-1978, 2019.doi:[[[10.1109/tcyb.2018.2817631]]]
- 8 J. Wu, X. Shen, and K. Jiao, "Game-based memetic algorithm to the vertex cover of networks," IEEE Trans. Cybern., vol. 49, no. 3, pp. 974-988, 2019.doi:[[[10.1109/tcyb.2018.2789930]]]
- 9 J. Chen and X. Li, "Toward the minimum vertex cover of complex networks using distributed potential games," Sci. China Inform. Sci., vol. 66, no. 1, pp. 1-20, 2023.doi:[[[10.1007/s11432-021-3291-3]]]
- 10 F. H. Thomas, "Attitudes toward risk and the risk-return paradox: Prospect theory explanations," Academy of Management J., vol. 31, no. 1, pp. 85-106, 1988.doi:[[[10.2307/256499]]]
- 11 J. S. Levy, "Prospect theory, rational choice, and international relations," Int. Studies Quart., vol. 41, no. 1, pp. 87-112, 1997.doi:[[[10.1111/0020-8833.00034]]]
- 12 D. Kahneman and A. Tversky, "Prospect theory: An analysis of decision under risk," Econometrica, vol. 47, no. 2, pp. 263-291, 1979.doi:[[[10.1017/cbo9780511803475.003]]]
- 13 L. Xiao, N. B. Mandayam, and H. Vincent Poor, "Prospect theoretic analysis of energy exchange among microgrids," IEEE Trans. Smart Grid, vol. 6, no. 1, pp. 63-72, 2015.doi:[[[10.1109/tsg.2014.2352335]]]
- 14 K. Jhala, B. Natarajan, and A. Pahwa, "Prospect theory-based active consumer behavior under variable electricity pricing," IEEE Trans. Smart Grid, vol. 10, no. 3, pp. 2809-2819, 2019.doi:[[[10.1109/tsg.2018.2810819]]]
- 15 M. J. Vahid-Pakdel, S. Ghaemi, B. Mohammadi-ivatloo, J. Salehi, and P. Siano, "Modeling noncooperative game of GENCOs’ participation in electricity markets with prospect theory," IEEE Trans. Ind. Informat., vol. 15, no. 10, pp. 5489-5496, 2019.doi:[[[10.1109/tii.2019.2902172]]]
- 16 Y . Wang, W. Saad, N. B. Mandayam, and H. V . Poor, "Load shifting in the smart grid: To participate or not?" IEEE Trans. Smart Grid, vol. 7, no. 6, pp. 2604-2614, 2016.doi:[[[10.1109/tsg.2015.2483522]]]
- 17 S. R. Etesami, W. Saad, N. B. Mandayam, and H. V . Poor, "Stochastic games for the smart grid energy management with prospect prosumers," IEEE Trans. Autom. Control, vol. 63, no. 8, pp. 2327-2342, 2018.doi:[[[10.1109/tac.2018.2797217]]]
- 18 W. Saad, A. Sanjab, Y . Wang, C. A. Kamhoua, and K. A. Kwiat, "Hardware trojan detection game: A prospect-theoretic approach," IEEE Trans. Veh. Technol., vol. 66, no. 9, pp. 7697-7710, 2017.doi:[[[10.1109/tvt.2017.2686853]]]
- 19 X. Li and X. Li, "Perception effect in evolutionary vaccination game under prospect-theoretic approach," IEEE Trans. Comput. Social Syst., vol. 7, no. 2, pp. 329-338, 2020.doi:[[[10.1109/tcss.2019.2960818]]]
- 20 G. Liao, X. Chen, and J. Huang, "Prospect theoretic analysis of privacy-preserving mechanism," IEEE/ACM Trans. Netw., vol. 28, no. 1, pp. 71-83, 2020.doi:[[[10.1109/tnet.2019.2951713]]]
- 21 A. Thanou, E. E. Tsiropoulou, and S. Papavassiliou, "Quality of experience under a prospect theoretic perspective: A cultural heritage space use case," IEEE Trans. Comput. Social Syst., vol. 6, no. 1, pp. 135-148, 2019.doi:[[[10.1109/tcss.2018.2890276]]]
- 22 H. Liu, Y . Song, and G. Yang, "Cross-efficiency evaluation in data envelopment analysis based on prospect theory," Eur. J. Oper. Res., vol. 273, no. 1, pp. 364-375, 2019.doi:[[[10.1016/j.ejor.2018.07.046]]]
- 23 A. Tversky and D. Kahneman, "Advances in prospect theory: Cumulative representation of uncertainty," J. Risk and Uncertainty, vol. 5, no. 4, pp. 297-323, 1992.doi:[[[10.1007/978-3-319-20451-2_24]]]
- 24 G. A. Quattrone and A. Tversky, "Contrasting rational and psychological analyses of political choice," Amer. Political Sci. Review, vol. 82, no. 3, pp. 719-736, 1988.doi:[[[10.1017/cbo9780511803475.026]]]
- 25 A. Tversky and D. Kahneman, Choices, values, and frames. Cambridge University Press, 2000.doi:[[[10.1037/0003-066X.39.4.341]]]
- 26 D. Prelec, "The probability weighting function," Econometrica, vol. 66, no. 3, pp. 497-528, 1998.doi:[[[10.2307/2998573]]]
- 27 A. Karci and A. Arslan, "Bidirectional evolutionary heuristic for the minimum vertex-cover problem," Comput. Elect. Eng., vol. 29, no. 1, pp. 111-120, 2003.doi:[[[10.1016/s0045-7906(01)00018-0]]]
- 28 P. S. Oliveto, J. He, and X. Yao, "Analysis of the (1+1)-ea for finding approximate solutions to vertex cover problems," IEEE Trans. Evol. Comput., vol. 13, no. 5, pp. 1006-1029, 2009.doi:[[[10.1109/tevc.2009.2014362]]]
- 29 J. F. Nash, "Equilibrium points in n-person games," Proc. Nat. Acad. Sci., vol. 36, no. 1, pp. 48-49, Jan. 1950.doi:[[[10.4337/9781781956298.00007]]]
- 30 G. W. Brown, "Iterative solution of games by fictitious play," Activity Anal. Prod. Allocation, vol. 13, no. 1, pp. 374-376, 1951.custom:[[[-]]]
- 31 T. Sandholm, A. Gilpin, and V . Conitzer, "Mixed-integer programming methods for finding Nash equilibria," in Proc. AAAI, 2005.custom:[[[https://www.cs.cmu.edu/~sandholm/MIPNash.aaai05.pdf]]]
- 32 R. Porter, E. Nudelman, and Y . Shoham, "Simple search methods for finding a Nash equilibrium," Games Econ. Behavior, vol. 63, no. 2, pp. 642-662, 2008.doi:[[[10.1016/j.geb.2006.03.015]]]
- 33 S. Benkessirat, N. Boustia, and R. Nachida, "A new collaborative filtering approach based on game theory for recommendation systems," J. Web Eng., pp. 303-326, 2021.doi:[[[10.13052/jwe1540-9589.2024]]]
- 34 V . Conitzer, "Approximation guarantees for fictitious play," in Proc. 47th Annual Allerton Conference on Communication, Control, and Computing, 2010.doi:[[[10.1109/allerton.2009.5394918]]]
- 35 D. Fudenberg and D. K. Levine, "Consistency and cautious fictitious play," J. Econ. Dynamics and Control, vol. 19, pp. 1065-1089, 1995.doi:[[[10.1016/0165-1889(94)00819-4]]]
- 36 P. Erd˝ os and A. R´ enyi, "On the evolution of random graphs," Publ. Math. Inst. Hung. Acad. Sci, vol. 5, no. 1, pp. 17-60, 1960.doi:[[[10.1515/9781400841356.38]]]
- 37 D. J. Watts and S. H. Strogatz, "Collective dynamics of ‘small-world’ networks," Nature, vol. 393, no. 6684, pp. 440-442, 1998.doi:[[[10.1038/30918]]]
- 38 A.-L. Barab´ asi and R. Albert, "Emergence of scaling in random networks," Sci., vol. 286, no. 5439, pp. 509-512, 1999.doi:[[[10.1515/9781400841356.349]]]
- 39 J. Wang, W. Li, S. Li, and J. Chen, "On the parameterized vertex cover problem for graphs with perfect matching," Sci. China Inform. Sci., vol. 57, no. 7, pp. 1-12, 2014.doi:[[[10.1007/s11432-013-4845-2]]]
- 40 Z. Qiu and P. Wang, "Parameter vertex method and its parallel solution for evaluating the dynamic response bounds of structures with interval parameters," Sci. China Physics, Mech. Astronomy, vol. 61, no. 6, pp. 064612, 2018.doi:[[[10.1007/s11433-017-9164-6]]]