Thuan Nguyen , Duong Nguyen-Huu and Thinh Nguyen
Achievable Zero-Error Rate Regions using Novel Location Assisted Coding (LAC) for Short Range FSO Communications
Abstract: Recent free-space optical (FSO) communication technologies have demonstrated the feasibility of building WiFO, a high capacity indoor wireless network using the femtocell architecture. In this paper, we introduce a cooperative transmission framework using location assisted coding (LAC) technique to increase the overall wireless capacity. For a given network topology, LAC provides three different schemes with different coding/decoding procedures. Based on these schemes, achievable zero-error rate regions for WiFO using LAC will be characterized. Both numerical and theoretical analyses are given to validate the proposed coding schemes.
Keywords: Achievable rate regions , coding , free space optical communication , wireless network
I. INTRODUCTION
THE number of wireless devices are projected to continue to grow significantly in the near future, fueled by the emerging markets for smart homes and the Internet of things (IoT). However, such an increase is anticipated to be hindered by the limited radio frequency (RF) spectrum. On the other hand, recent advances in free space optical (FSO) technology promise a complementary approach to increase wireless capacity with minimal changes to the existing wireless technologies. The solid state light sources such as lighting emitting diode (LED) and vertical cavity surface emitting laser (VCSEL) are now sufficiently mature that it is possible to transmit data at high bit rates reliably with low energy consumption using simple modulation schemes such as on-off keying. Importantly, the FSO technologies do not interfere with the RF transmissions. However, such high data rates are currently achievable only with point-to-point transmissions and not well integrated with existing WiFi systems. This drawback severely limits the mobility of the free space optical wireless devices.
In [1]–[4], the authors proposed an indoor WiFi-FSO hybrid communication system called WiFO that promises to provide orders of magnitude improvement in bandwidth while maintaining the mobility of the existing WiFi systems. WiFO aims to alleviate the bandwidth overload problem often associated with existing WiFi systems at crowded places such as airport terminals or conference venues. WiFO modulates invisible LED light to transmit data in localized light cones to achieve high bit rate with minimal interference.
alleviate the bandwidth overload problem often associated with existing WiFi systems at crowded places such as airport terminals or conference venues. WiFO modulates invisible LED light to transmit data in localized light cones to achieve high bit rate with minimal interference.
II. RELATED WORK
From the FSO communication perspective, our work is related to several studies on FSO/RF hybrid systems [5]–[8]. The majority of these studies, however are in the context of outdoor point-to-point FSO transmission, using a powerful modulated laser beam. To obtain high bit rates and spectral efficiency, many FSO communication systems [9] use sophisticated modulation schemes such as phase-shift keying (PSK) or quadrature phase-shift keying (QPSK) [10], [11] or quadrature amplitude modulation (QAM) [12], [13] or pulse position modulation (PPM) [14], [15]. However, these modulation schemes pay high costs in power consumption, complexity, and additional sensitivity to phase distortions of the received beam [16]. In contrast, taking the advantage of high modulation bandwidth of recent LED/VCSEL and short-range indoor transmissions, our work uses simple pulse amplitude modulation (PAM) [17], specifically on-off keying which results in simplicity and low power consumption.
From the coding’s perspective, the proposed LAC technique inWiFO is similar to MIMO systems that have been used widely in communication systems to improve the capacity [18]–[24]. Both LAC and MIMO techniques use several transmitters to transmit signals to achieve higher capacity. However, using multiple transmitters at the same time can also cause interference among transmissions to different receivers if they are in the same transmission range. As such, a MIMO receiver typically receives signals from multiple transmit antennas and these signals are intended for that particular MIMO receiver at any time slot. On the other hand, in WiFO, multiple transmitters transmit the joint messages simultaneously to multiple WiFO receivers, rather than a single receiver. By taking advantage of the known interference patterns using the receiver location information, LAC technique can help WiFO receivers to decode each message independently in presence of interference. We note that a special case of LAC technique was first introduced in [4]. In this paper, we extend and improve the LAC technique to obtain higher rates.
We note that our problem of characterizing the achievable zero-error capacity region appears to be similar to the wellknown degraded broadcast channels (DBCs) [25], [26] whose capacities have been established. However, WiFO channel is not a DBC, and thus the well-known results on DBC are not applicable [27]. In addition, the WiFO channel is a special case of deterministic discrete memoryless broadcast channels (DMBCs) [28]. The achievable inner bound (Shannon) capacity regions for deterministic DMBCs have been studied previously. On the other hand, no explicit coding method to achieve these inner bounds was given [28]. In contrast, our work considers the zero-error capacity rather than the classic Shannon capacity. Our work also provide an explicit constructive coding technique using the short length codewords. Consequently it is computational efficient and resulted in short coding delay.
Finally, our work appears to be similar to analog network coding (ANC) [29], [30]. Using ANC, a receiver has access to the side information and uses it to increase the transmission rate. On the other hand, using LAC, a receiver does not need side information. Instead, the AP has all the data wanted by all the receivers and their locations. It uses this information to encode the bits in a way that allows simple decoding at the receivers.
III. PRELIMINARIES: OVERVIEW OF WIFO ARCHITECTURE
To transmit data, each FSO transmitter creates an invisible light cone about one square meter directly below in which the data can be received. Fig. 1(a) shows a typical coverage area of WiFO using several FSO transmitters. Digital bits “1” and “0” are transmitted by switching the LEDs on and off rapidly. For the general PAM scheme, signals of more than two levels can be transmitted by varying the LED intensities. The switching rate of the current system can be up to 100 MHz for LED-based transmitters and > 1 GHz for VCSEL-based transmitters. We note that, a number of existing FSO systems use visible light communication (VLC) which limits the modulating rate of a transmitter. Thus, to achieve high bit rates, these systems use highly complex demodulators and modulators (e.g. 64-QAM, OFDM), which make them less energy efficient. Fig. 1(b) shows the light intensity as the function of the position measured from
Fig. 1.
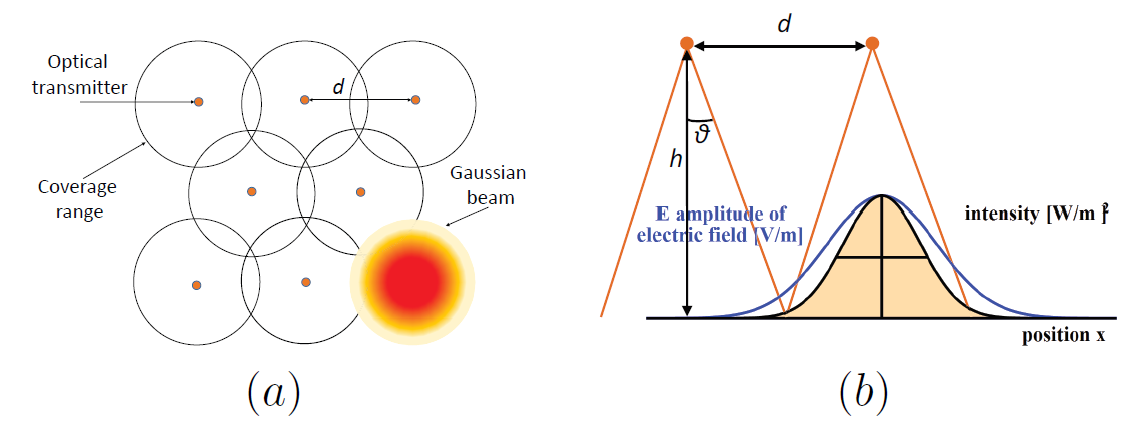
the center of the cone. High intensity results in more reliable transmissions.
All the FSO transmitters are connected to a 100 Gbps Ethernet network which is controlled by the Access Point (AP). The AP is the brain of the WiFO system that controls the simultaneous data transmissions of each FSO transmitter and the existing WiFi channel. At the receiving side, each WiFO receiver is equipped with a silicon pin photodiode which converts light intensity into electrical currents that can be interpreted as the digital bits “0” and “1”. The AP decides whether to send a packet on the WiFi or FSO channels. If it decides to send the data on the FSO channel for a particular device, the data will be encoded appropriately, and broadcast on the Ethernet network with the appropriate information to allow the right device to transmit the data.
A salient feature of WiFO is that, in a dense deployment scenario where light cones from LEDs are overlapped, a single receiver can associate with multiple LEDs. As will be shown in Section IV, using cooperative transmissions from these LEDs via a novel location assisted coding (LAC) technique, a receiver in an overlapped area can receive higher bit rates. Importantly, we note that LAC is a high-level coding technique similar to network coding technique that assumes low bit error rate of the lower-layer links (physical link). This assumption holds in high SNR regimes, or can be made to hold using sufficient amount of forward error correction at the expense of lowering the information rate.
IV. PROBLEM DESCRIPTION
In this section, we first provide some of the basic assumptions on the capabilities of WiFO.
A. Assumption
Location Knowledge. The AP knows the locations of all receivers, i.e., it knows which light cone that a receiver is currently located in. This is accomplished through the WiFO’s mobility protocol [31].
Sparse vs. Dense Deployment. Sparse deployment of FSO transmitters results in less FSO coverage, but is resource efficient. On the other hand, a dense deployment increases mobility and the bit rates for a single receiver if two or more transmitters are used to transmit data to a single receiver. However, a dense deployment also leads to multi-user interference that might reduce the overall rate. In this paper, we are interested in dense deployment scenarios and show that the multi-user interference can be significantly reduced when the knowledge of receiver lo
cations is incorporated into the proposed cooperative transmission scheme or LAC technique.
Transmitter. There are n FSO transmitters [TeX:] $$T_{1}, T_{2}, \cdots, T_{n},$$ each produces a light cone that overlaps each other. There are also m receivers denoted as [TeX:] $$R_{1}, R_{2}, \cdots R_{m}.$$ A FSO transmitter is assumed to use PAM for transmitting data. However, to simplify our discussion, we will assume that a sender uses on-off keying (OOK) modulation where high power signal represents “1” and low power signal represents “0” [16]. We note that the proposed LAC scheme can be easily extended for PAM.
Receiver. A receiver is assumed to be able to detect different levels of light intensities. If two transmitters send a “1” simultaneously to a receiver, the receiver would be able to detect “2” as light intensities from two transmitters add constructively. On the other hand, if one transmitter sends a “1” while the other sends a “0”, the receiver would receive a “1”.
We assume that the light intensity is approximately the same in the overlapped area after performing a coarse quantization. The receiver in the overlapped area of two active transmitters has the normalized/quantized light intensity of 2. The receiver in the coverage area of only one transmitter has the quantized light intensity of 1, and the receiver that is not in the coverage area of any transmitter, has the quantized light intensity of 0. This is due to the additive model of light intensity that has been empirically verified. Fig. 2 shows a typical light intensity as a function of the distance when two neighboring transmitters are active. As seen, the light intensity in the overlapped area is large as a result of adding two light sources. While the light intensity in the single coverage is smaller, and the light intensity in the non-coverage area is smallest.
B. Channel Model
To illustrate our channel model, we consider a simple topology with two transmitters [TeX:] $$T_{1}, T_{2}$$ and two receivers [TeX:] $$R_{1}, R_{2}$$ in Fig. 3 (a). Using OOK modulation, the transmitted signal at each transmitter is [TeX:] $$\in\{0,1\}.$$ The receiver [TeX:] $$R_{2}$$ is in the overlapped area, and therefore can receive the signals from both transmitters while receiver [TeX:] $$R_{1}$$ can receive signal from only one transmitter.
A cooperative transmission scheme uses both transmitters to send independent information to each receiver simultaneously. This cooperative transmission scheme can be viewed as a broadcast channel in which the sender can broadcast four possible symbols: “00”, “01”, “10”, and “11” with the left and right bits
Fig. 3.

Fig. 4.

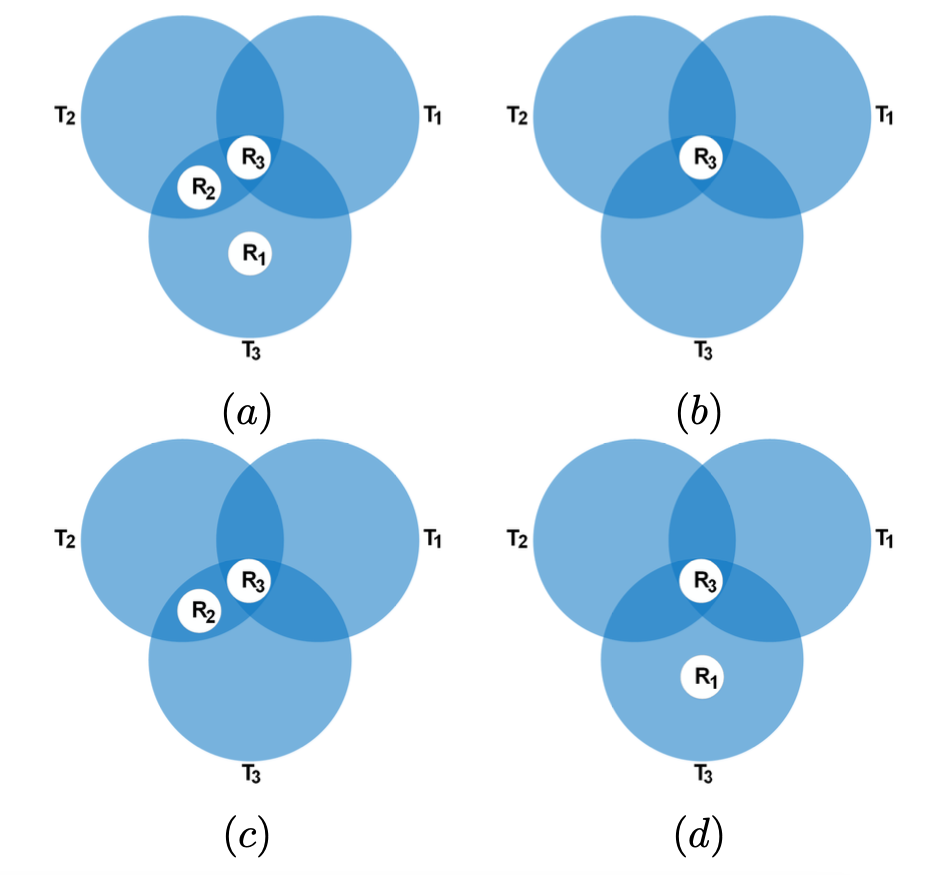
are transmitted by different transmitters. Thus, there is a different channel associated with each receiver depending on their locations. Fig. 3(b) shows the broadcast channel for the two receivers [TeX:] $$R_{1} \text { and } R_{2}.$$ There are only three possible symbols for [TeX:] $$R_{2}$$ because it is located in the overlapped coverage of two transmitters. Therefore, it cannot differentiate the transmitted patterns “01” and “10” as both transmitted patterns result in a “1” at [TeX:] $$R_{2}$$ due to the additive interference. On the other hand, there are only two symbols at receiver [TeX:] $$R_{1}$$ because it is located in the coverage of a single transmitter. Similarly, Fig. 4(a) shows a topology with three transmitters and two receivers and Fig. 4(b) shows the corresponding broadcast channels.
We assume that channel errors are either negligible or can be made negligible using forward error correcting (FEC) codes. In fact, measurement results of our current WiFO prototype show that the bit error rate is negligible for transmission distance of less than 2 meters. When moderately strong FEC such as RS (255, 223) is applied, the resulted bit error rate is virtually zero up to 3 meters. Thus, LAC can be viewed as a high level coding scheme such as network coding where the received symbols (“0”, “1”, “2”, etc.) at the physical layers are assumed to be correct. Based on this assumption, all errors are due to interference. Thus, the channel matrices for [TeX:] $$R_{1} \text { and } R_{2}$$ associated with Fig. 3(b) are:
We note that the entry A(i, j) denotes probability that a transmitted symbol i to turn a symbol j at the receiver. A(i, j) is either 0 or 1 which denote whether interference occur or not.
Similarly, the channel matrices for [TeX:] $$R_{1} \text { and } R_{2}$$ associated with Fig. 4(b) are:
C. Achievable Zero-Error Rate Region
Achievable zero-error rate region characterizes the joint rates that each receiver can receive their independent information without error. For convenience, in this paper we will refer achievable zero-error rate as simply achievable rate. Our goal is to determine a cooperative transmission scheme among the transmitters in order to enlarge the achievable rate region for the receivers.
Fig. 3(a) shows an example topology under consideration. We assume that transmitters [TeX:] $$T_{1} \text { and } T_{2}$$ are responsible for transmitting independent information to its receivers [TeX:] $$R_{1} \text { and } R_{2}$$ respectively. Suppose [TeX:] $$R_{1} \text { and } R_{2}$$ want to receive bits “1” and “0”, respectively. If [TeX:] $$T_{1} \text { and } T_{2}$$ transmit bit “1” and “0”, respectively, then [TeX:] $$R_{1}$$ will correctly receive its bit “1”. On the other hand, since [TeX:] $$R_{2}$$ is located in the overlapped coverage of [TeX:] $$T_{1} \text { and } T_{2},$$ it will incorrectly receive bit “1” due to interference. To resolve the multi-user interference, each transmitter can take turn to transmit a bit to its receiver in each time slot. Using this TDMA, each receiver can receive 0.5 bit per time slot on the average. Another scheme would be to transmit bits to either [TeX:] $$R_{1}$$ or [TeX:] $$R_{2}$$ exclusively. This implies that one receiver will obtain one bit while the other has zero bit per time slot. Let (x, y) denote the achievable rate tuple where x and y denote the average rate of [TeX:] $$R_{1} \text { and } R_{2} \text {, }$$ then the achievable rate region include the rate tuples: (1,0), (0,1), (0.5,0.5). In general, a time-sharing strategy that uses the scheme (1,0) for [TeX:] $$\lambda$$ fraction of the time, and the scheme (0,1) for [TeX:] $$1-\lambda$$ of the time produces a rate region shown in Fig. 5. In Section V, we will show that such a scheme produces a suboptimal rate region, and describe how the proposed LAC technique can be used to enlarge the achievable rate region.
V. COOPERATIVE TRANSMISSION VIA LOCATION ASSISTED CODING (LAC)
LAC is a cooperative transmission scheme that uses the receiver’s location information to enlarge the achievable rate region. For a given topology, LAC employs different coding schemes: Single rate coding (SRC), equal rate coding (ERC), and joint rate coding (JRC). Each scheme finds a different feasible rate tuple. Next, by varying the fractions of the time that LAC uses these different coding schemes, the achievable rate region can be achieved as the convex hull of these rate tuples.
A. Single Rate Coding
Using SRC, a receiver in the coverage of n transmitters, can receive a larger bit rate by using all n transmitters to transmit the information for that particular receiver. As a result, other receivers even though located in the coverage of some of these n transmitters, will not receive any information. We have the following results on the achievable rate of the single receiver.
Proposition 1: (Single Rate Coding) For a receiver in the light cone of n transmitters, the achievable rate is log (n + 1) bits per time slot.
Proof. Since each transmitter is capable of transmitting “0” or “1” only, and the single receiver receives the sum of all the signals from the n transmitters, then there is total of n + 1 distinct levels perceived at the receiver. Furthermore, since there is no error involved, the probability mass function of the transmitted symbols is identical of the probability mass function of the received symbols. Thus, from basic result of information theory [32], the capacity for the single user is achieved using the uniform probability mass function which results in log (n + 1) bits per time slot. Note that the rates of other receivers is zero.
B. Equal Rate Coding
Using SRC, a single receiver can obtain a large bit rate while rates for other receivers are zero. On the other hand, using ERC, for certain topologies, each receiver can obtain one independent bit per time slot. Let H to be the topology matrix whose entry H(i, j) is equal to 1 if receiver i can receive signal from transmitter j and 0 otherwise. For example, the topology matrix associated with Fig. 3(a) is:
Assume that H is full rank and the number of receivers equal to the number of transmitters, then we have following proposition from our previous work [4]:
Proposition 2: (Equal rate coding [4])
1. If a [TeX:] $$n \times n$$ topology matrix H is full-rank, then using ERC, every receiver can receive one bit per time slot.
2. Furthermore, ERC maximizes the sum rate of all receivers at n bits per time slot.
Proof. We will show explicitly the encoding and decoding procedures to obtain one bit per time slot for each receiver using ERC.
Encoding: Let [TeX:] $$b=\left(b_{1}, b_{2}, \cdots, b_{n}\right)^{T}$$ denote the information bits intended to be sent to receiver [TeX:] $$R_{1}, R_{2}, \cdots, R_{n},$$ respectively. [TeX:] $$x= \ \left(x_{1}, x_{2}, \cdots, x_{n}\right)^{T},$$ respectively, and [TeX:] $$y=\left(y_{1}, y_{2}, \cdots, y_{n}\right)^{T}$$ be the signal received at the receiver [TeX:] $$R_{i}.$$ The goal of the encoding scheme x = C(b), is to produce the bits [TeX:] $$x_{i} \text { 's }$$ such that every receiver [TeX:] $$R_{i},$$ upon receiving [TeX:] $$y_{i},$$ can recover its [TeX:] $$b_{i}.$$
We consider the following system of linear equations:
(1)
[TeX:] $$\left\{\begin{aligned} H(1,1) x_{1} \oplus H(1,2) x_{2} \oplus \cdots \oplus H(1, n) x_{n} &=b_{1} \\ H(2,1) x_{1} \oplus H(2,2) x_{2} \oplus \cdots \oplus H(2, n) x_{n} &=b_{2} \\ & \ldots \\ H(n, 1) x_{1} \oplus H(n, 2) x_{2} \oplus \cdots \oplus H(n, n) x_{n} &=b_{n} \end{aligned}\right.,$$where [TeX:] $$\oplus$$ is addition in the Galois field 2 (GF(2)) with two elements “0” and “1”, i.e. [TeX:] $$a \oplus b=(a+b)$$ mod 2. Since H is full-rank in GF(2), we can solve the system of equations (1) above for unique [TeX:] $$x_{1}, x_{2}, \cdots, x_{n}$$ in terms of [TeX:] $$b_{1}, b_{2}, \cdots, b_{n}.$$ Mathematically, the encoding is:
where all computations are done in finite field GF(2). Next, each transmitter [TeX:] $$T_{i}$$ transmits [TeX:] $$x_{i} ' s$$ to the receivers.
Decoding: A receiver [TeX:] $$R_{i}$$ needs to be able to recover bit [TeX:] $$b_{i}$$ from the received signal [TeX:] $$y_{i}$$ which can be represented as:
(3)
[TeX:] $$\left\{\begin{array}{l} y_{1}=H(1,1) x_{1}+H(1,2) x_{2}+\cdots+H(1, n) x_{n} \\ y_{2}=H(2,1) x_{1}+H(2,2) x_{2}+\cdots+H(2, n) x_{n} \\ \quad \cdots \\ y_{n}=H(n, 1) x_{1}+H(n, 2) x_{2}+\cdots+H(n, n) x_{n}, \end{array}\right.$$
It is easy to check that [TeX:] $$b_{i}=\hat{b}_{i}.$$ This can be seen by performing mod 2 operations on both sides of equations (3) which results in equations (1). Or simply, if [TeX:] $$y_{i}$$ is even then [TeX:] $$R_{i}$$ decodes bit [TeX:] $$b_{i}$$ as “0”, and “1” otherwise. Consequently, each receiver can decode its bits correctly and independently in presence of interference. Due to all the transmitted bits can be decoded correctly and independently, the equal rate decoding (ERC) can provide the transmission rate of n bit per time slot.
Noting that the sum rate is upper bounded by the maximum number of independent bits that can be sent out simultaneously. Since there are n transmitters, there are at most n bits can be sent out simultaneously. We have already showed that for a full rank [TeX:] $$n \times n$$ H, each of the n receivers can receive one bit per time slot. Thus, using ERC results in a maximum rate of n bits per time slot which confirms the second statement of Proposition 2.
We note that since the transmitter is only capable to sending “0” or “1”, the system of equations (1) mus be operated in GF(2) to produce the encoded bits [TeX:] $$b_{i} \in\{0,1\} \text {. }$$ That said, the ERC coding schemes can be extended to a general PAM signal in the following way. Assume that the transmitters can transmit with k levels from 0 to k 1 where k is a prime number, and the topology matrix is full-rank, then the ERC coding scheme can be extended to GF(k). The proof is similar to the proof for the case of GF(2) by replacing all the computations [TeX:] $$a \oplus b$$ with (a + b) mod k. Since the topology matrix is still invertible, all the transmitted bits can be decoded correctly and ERC can provide the transmission rate of n bits per time slot.
Fig. 6.
C. Joint Rate Coding
Proposition 2 establishes the sufficient conditions regarding the topology that allows for (1) independent information to be sent at equal rates to all receivers and (2) achieving maximum sum rate. Now, we describe the joint rate coding (JRC) technique that allows receivers to obtain different rates. We use the following definitions and notations.
Definition 1: (Exclusive and shared transmitters)
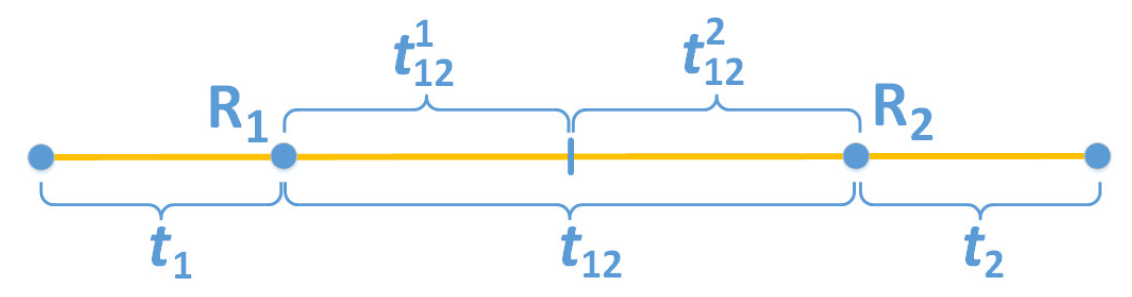
Let [TeX:] $$\mathcal{R}=\{1,2, \cdots, m\}$$ be the set of m receivers, [TeX:] $$\mathcal{S} \subset \mathcal{R},$$ and [TeX:] $$\mathcal{T}_{\mathcal{S}}$$ denotes a group of transmitters that cover exactly all the receivers in S. Each transmitter in [TeX:] $$\mathcal{T}_{\mathcal{S}}$$ is called an exclusive transmitter if [TeX:] $$\mathcal{S}$$ is a singleton, and a shared transmitter if [TeX:] $$\mathcal{S}$$ has two or more elements. Let [TeX:] $$t_{\mathcal{S}}=\left|\mathcal{T}_{\mathcal{S}}\right|$$ denote the number of transmitters, each covers exactly all the receivers in [TeX:] $$\mathcal{S} .$$ We use [TeX:] $$t_{i}$$ to denote the number of transmitters that covers the receiver [TeX:] $$R_{i}$$ exclusively while [TeX:] $$t_{i j}$$ denotes the number of pairwise sharing transmitters that cover only two receivers [TeX:] $$R_{i} \text { and } R_{j}$$ and no other receivers.
In Fig. 3(a), transmitter [TeX:] $$T_{2}$$ is the only exclusive transmitter for [TeX:] $$R_{2}, \text { and so } t_{2}=1 \text {. }$$ On the other hand, [TeX:] $$t_{1}=0$$ since there is no exclusive transmitter for [TeX:] $$R_{1}.$$ However, [TeX:] $$T_{1}$$ is a shared transmitter between [TeX:] $$R_{1} \text { and } R_{2}, \text { so } t_{12}=1.$$ Similarly, in Fig. 4(a), [TeX:] $$t_{1}=0 \ t_{2}=2, \text { and } t_{12}=1.$$
The key to the JRC technique is how to use the shared transmitters to transmit bits to multiple receivers simultaneously. At the fundamental level, we develop JRC technique for topologies that consist only exclusive and pairwise sharing transmitters. Figs. 3(a) and 4(a) show such topologies. We then show how to decompose a general topologies into the several pairwise sharing topologies, then the fundamental techniques for pairwise can be applied. We will first consider a two receivers [TeX:] $$R_{1} \text { and } R_{2} \text { with } t_{1} \text { and } t_{2}$$ exclusive transmitters and [TeX:] $$t_{12}$$ shared transmitters.
JRC allocates different rates to the receivers [TeX:] $$R_{1} \text { and } R_{2}$$ through two parameters, which can be viewed as the number of shared transmitters allocated to [TeX:] $$R_{1} \text { and } R_{2}.$$ In particular, we denote [TeX:] $$t_{12}^{1} \text { and } t_{12}^{2}$$ as the number of shared transmitters allocated to [TeX:] $$R_{1} \text { and } R_{2} \text {, }$$ respectively. We have:
We will show that by increasing [TeX:] $$t_{12}^{1},$$ we allow [TeX:] $$R_{1}$$ to achieve a higher rate at the expense of a reduced rate for [TeX:] $$R_{2}.$$ Fig. 6 illustrates our notations. We have the following proposition on the achievable rates using JRC for two receivers.
Proposition 3: (Achievable rates for two-receiver topology). If [TeX:] $$t_{1} \geq t_{12}^{2} \text { and } t_{2} \geq t_{12}^{1}$$ then [TeX:] $$R_{1} \text { and } R_{2}$$ can achieve the rates of [TeX:] $$\log c_{1}=\log \left(t_{1}+t_{12}^{1}+1\right) \text { and } \log c_{2}=\log \left(t_{2}+t_{12}^{2}+1\right)$$ bits per time slot, respectively, where [TeX:] $$t_{12}^{1}+t_{12}^{2} \leq t_{12} . t_{12}^{1} \text { and } t_{12}^{2}$$ are parameters that control the rates between [TeX:] $$R_{1} \text { and } R_{2}.$$
Note that to maximize the rates, we want [TeX:] $$t_{12}^{1}+t_{12}^{2}=t_{12}.$$
Proof. We will describe a constructive proof for Proposition 3. But first, let [TeX:] $$x_{12}$$ be a non-negative integer represented by the bit patterns sent out by [TeX:] $$t_{12}$$ shared transmitters. Since each shared transmitter can send either a “0” or “1”, [TeX:] $$x_{12}$$ has [TeX:] $$t_{12}+1$$ levels, i.e., [TeX:] $$x_{12} \in\left\{0,1, \cdots, t_{12}\right\}.$$ Let [TeX:] $$x_{i}$$ be a nonnegative integer that represents the bit patterns transmitted by [TeX:] $$t_{i}$$ exclusive transmitters for receiver [TeX:] $$R_{i} . x_{i} \text { has } t_{i}+1$$ levels, i.e., [TeX:] $$x_{i} \in\left\{0,1, \cdots, t_{i}\right\} . \text { Let } y_{i}$$ be a non-negative integer that represents the signal received by the receiver [TeX:] $$R_{i}.$$ Due to additive property, we have:
Next, we note that the achievable rate of [TeX:] $$R_{i}$$ is log of the number of symbols (levels) that [TeX:] $$R_{i}$$ can distinguish per time slot. Let [TeX:] $$c_{i}$$ be a non-negative integer representing the number of distinguishable levels at [TeX:] $$R_{i},$$ then log [TeX:] $$c_{i}$$ is the achievable rate of [TeX:] $$R_{i}.$$ We will show that if [TeX:] $$t_{1} \geq t_{12}^{2} \text { and } t_{2} \geq t_{12}^{1},$$ then it is possible to send any arbitrary pattern pair [TeX:] $$\left(b_{1}, b_{2}\right)$$ to the receiver [TeX:] $$R_{1}$$ and [TeX:] $$R_{2}$$ without any error, with
This would establish the proof for Proposition 3. We now describe the encoding and decoding procedures, then verify their correctness.
Encoding: Suppose we want to transmit the pattern [TeX:] $$\left(b_{1}, b_{2}\right)$$ to [TeX:] $$\left(R_{1}, R_{2}\right),$ respectively. Then, the encoding is a function that maps [TeX:] $$\left(b_{1}, b_{2}\right)$$ into [TeX:] $$x_{1}^{*}, x_{2}^{*} \text {, and } x_{12}^{*} \text {,i.e., }\left(x_{1}^{*}, x_{2}^{*}, x_{12}^{*}\right)= \ \mathcal{C}\left(b_{1}, b_{2}\right).$$ Let the set [TeX:] $$\left\{x_{12}\left(b_{1}\right)\right\}$$ parameterized by [TeX:] $$b_{1}$$ consisting of [TeX:] $$t_{1}+1$$ elements be defined as:
(7)
[TeX:] $$\left\{x_{12}\left(b_{1}\right)\right\}=\left\{b_{1}-i_{1} \quad \bmod \left(c_{1}\right), i_{1}=0,1, \cdots, t_{1}\right\}.$$Similarly, let the set [TeX:] $$\left\{x_{12}\left(b_{2}\right)\right\}$$ parameterized by [TeX:] $$b_{2}$$ consisting of [TeX:] $$t_{2}+1$$ elements be defined as:
(8)
[TeX:] $$\left\{x_{12}\left(b_{2}\right)\right\}=\left\{b_{2}-i_{2} \quad \bmod \left(c_{2}\right), i_{2}=0,1, \cdots, t_{2}\right\}.$$We now encode [TeX:] $$b_{1}, b_{2} \text { into } x_{1}^{*}, x_{2}^{*} \text {, and } x_{12}^{*}$$ as follows. We pick [TeX:] $$x_{12}^{*}$$ to be the minimum value element in the intersection set of [TeX:] $$\left\{x_{12}\left(b_{1}\right)\right\} \text { and }\left\{x_{12}\left(b_{2}\right)\right\},$$ i.e., :
Next, we set [TeX:] $$x_{i}^{*}, i=1,2$$ to:
Decoding: [TeX:] $$R_{i}$$ receives the signal:
the sum of the signals transmitted by the exclusive transmitters and shared transmitters. [TeX:] $$R_{i}$$ decodes the transmitted level [TeX:] $$b_{i}$$ as:
To verify the correctness of encoding and decoding procedures, we need to verify (a) [TeX:] $$\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}$$ is non-empty that enables us to choose [TeX:] $$x_{12}^{*}=\min \left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\} ;$$ (b) [TeX:] $$x_{12}^{*} \leq t_{12}.$$ This is required since we want the [TeX:] $$t_{12}$$ shared transmitters to be able to represent [TeX:] $$x_{12}^{*} ; \text { (c) } 0 \leq x_{1}^{*} \leq t_{1}$$ and [TeX:] $$0 \leq x_{2}^{*} \leq t_{2}$$ to enable the exclusive transmitters to represent [TeX:] $$x_{i};$$ (d) [TeX:] $$\hat{b}_{i}=b_{i}$$ for the correctness of the decoding procedure.
First, we will verify the condition (a). From the definition ((7) and (8)), the sets [TeX:] $$\left\{x_{12}\left(b_{i}\right)\right\}$$ consists of [TeX:] $$\left(t_{i}+1\right)$$ distinct elements each. Furthermore,
The number of elements in [TeX:] $$\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}$$ set is:
Now since [TeX:] $$c_{1}=t_{1}+t_{12}^{1}+1 \text { and } c_{2}=t_{2}+t_{12}^{2}+1,$$ we have:
(12)
[TeX:] $$\left|\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}\right| \geq \min \left(t_{2}-t_{12}^{1}+1, t_{1}-t_{12}^{2}+1\right).$$Using the conditions in Proposition 3: [TeX:] $$t_{1} \geq t_{12}^{2} \text { and } t_{2} \geq t_{12}^{1},$$ we conclude the intersection set [TeX:] $$\left|\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}\right|$$ has at least one element, and therefore we can pick [TeX:] $$x_{12}^{*}.$$
Next, we will prove condition (b) by contradiction by assuming
Let [TeX:] $$x_{12}^{\max }$$ be the maximum element in [TeX:] $$\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\} .$$ Then,
(14)
[TeX:] $$\begin{aligned} x_{12}^{\max } & \geq x_{12}^{*}+\left|\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}\right|-1 \\ &>t_{12}+\left|\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}\right|-1 \end{aligned}$$
(15)
[TeX:] $$\begin{aligned} x_{12}^{\max } & \geq x_{12}^{*}+\left|\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}\right|-1 \\ &>t_{12}+\left|\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}\right|-1 \end{aligned}$$
(16)
[TeX:] $$\begin{aligned} &\geq \min \left(t_{12}^{1}+t_{12}^{2}+t_{2}-t_{12}^{1}, t_{12}^{1}+t_{12}^{2}+t_{1}-t_{12}^{2}\right) \\ &=\min \left(t_{2}+t_{12}^{2}, t_{1}+t_{12}^{1}\right) \\ &=\min \left(c_{2}-1, c_{1}-1\right) \end{aligned}$$where (14), (15) and (16) are due to (13), (12) and (5), respectively. Therefore, [TeX:] $$x_{12}^{\max }$$ is strictly greater than [TeX:] $$\min \left(c_{2}-1, c_{1}-\right. \ \text { 1). }$$ But this contradicts with the way we constructed the set [TeX:] $$\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}$$ whose maximum element cannot exceed min [TeX:] $$\left(c_{1}-1, c_{2}-1\right)$$ due to mod [TeX:] $$c_{1}$$ and mod [TeX:] $$c_{2}$$ operation in the encoding procedure. Therefore, [TeX:] $$x_{12}^{*}$$ must satisfy condition (b).
Next, due to [TeX:] $$x_{12}^{*} \in\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}$$ and from (7), (8), we have:
Therefore, from (9):
(17)
[TeX:] $$x_{i}^{*}=b_{i}-x_{12}^{*} \in\left\{0,1, \cdots, t_{i}\right\} \quad \bmod \left(c_{i}\right).$$This establishes the verification for (c).
The correctness of condition (d) can be easily seen by noting that [TeX:] $$b_{i}=\hat{b}_{i}$$ by combining (10), (11), and (17).
Noting that for given values of [TeX:] $$t_{1}, t_{2} \text { and } t_{12},$ we can adjust the rates to [TeX:] $$R_{1} \text { and } R_{2}$$ by changing the values of [TeX:] $$t_{12}^{1} \text { and } t_{12}^{2}.$$ From Proposition 3, for any [TeX:] $$t_{12}^{1} \text { and } t_{12}^{2}$$ such that [TeX:] $$t_{1} \geq t_{12}^{2}, t_{2} \geq t_{12}^{1}, \text { and } t_{12}^{1}+t_{12}^{2} \leq t_{12}, R_{1} \text { and } R_{2}$$ are possible to achieve the rates of [TeX:] $$\log \left(t_{1}+t_{12}^{1}+1\right) \text { and } \log \left(t_{2}+t_{12}^{2}+1\right)$$ bits per time slot, respectively. For example, if one wants to distribute a higher bit rate to [TeX:] $$R_{1},$$ the AP will increase the value of [TeX:] $$t_{12}^{1}$$ in order to achieve a larger value of [TeX:] $$\log \left(t_{1}+t_{12}^{1}+1\right).$$ However, due to the constraint [TeX:] $$t_{12}^{1}+t_{12}^{2} \leq t_{12},$$ a larger value of [TeX:] $$t_{12}^{1}$$ might lead to a smaller value of [TeX:] $$t_{12}^{2}$$ which results in a lower bit rate of [TeX:] $$\log \left(t_{2}+t_{12}^{2}+1\right) \text { for } R_{2}.$$
Example V.1: Fig. 4(a) shows an example of a topology consisting of three transmitters and two receivers. The number of exclusive transmitters for [TeX:] $$R_{1} \text { and } R_{2} \text { are } t_{1}=0 \text { and } t_{2}=2$$ while the number of shared transmitters [TeX:] $$t_{12}=1.$$ Choose [TeX:] $$t_{12}^{1}=1 \text { and } t_{12}^{2}=0,$$ then this pair is valid since:
Then, from Proposition 3, the achievable rate of [TeX:] $$R_{1}$$ is [TeX:] $$\log \left(t_{1}+t_{12}^{1}+1\right)=\log \left(c_{1}\right)=\log (2),$$ and for [TeX:] $$R_{2} \text { is } \log \left(t_{2}+\right. \ \left.t_{12}^{2}+1\right)=\log \left(c_{2}\right)=\log (3).$$ Therefore, [TeX:] $$R_{1}, R_{2}$$ can achieve arbitrary pattern [TeX:] $$\left(b_{1}, b_{2}\right) \text { with } b_{1} \in\{0,1\} \text { and } b_{2} \in\{0,1,2\} \text {, }$$ respectively.
For example, suppose that [TeX:] $$\left(b_{1}, b_{2}\right)=(1,2)$$ is the desired bit pattern for [TeX:] $$R_{1}, R_{2}.$$ The encoding and decoding procedures to find [TeX:] $$\left(x_{1}^{*}, x_{2}^{*}, x_{12}^{*}\right)=\mathcal{C}\left(b_{1}, b_{2}\right)$$ is shown below.
Encoding: Encoding procedure will construct two sets:
Then, [TeX:] $$\left\{x_{12}\left(b_{1}\right)\right\} \cap\left\{x_{12}\left(b_{2}\right)\right\}=\{1\}.$$ Choose [TeX:] $$x_{12}^{*}=1.$$ Next, construct [TeX:] $$x_{1} \text { and } x_{2}$$ as:
Hence, [TeX:] $$\left(x_{1}^{*}, x_{2}^{*}, x_{12}^{*}\right)=(0,1,1).$$
Decoding: Decoding procedure will decode by summing up all received signals at each receiver, i.e.,:
Similar to ERC, the JRC can be extended to arbitrary number of receivers. Next, we present the extended results for n receivers with pairwise sharing transmitters.
Proposition 4: (Achievable rates for n-receiver pairwise sharing transmitter topology) Given a topology consisting of n receivers [TeX:] $$R_{1}, R_{2}, \cdots, R_{n},$$ if each receiver [TeX:] $$R_{i} \text { has } t_{i}$$ exclusive transmitters and [TeX:] $$t_{i p}$$ sharing transmitters with other receiver [TeX:] $$R_{p}.$$ Then the receiver [TeX:] $$R_{i}$$ can achieve the rate:
bits per time slot, if with [TeX:] $$\forall p \in\{1, \cdots, n\} \text { and } p \neq i :$$
Note: In the case [TeX:] $$t_{i p}=0 \text {, i.e., } R_{i} \text { and } R_{p}$$ do not share any transmitter, then in the inequality, [TeX:] $$t_{p}$$ will be replaced by “0” or the number of sharing transmitters assigned to [TeX:] $$R_{i} \text { is } t_{i_{n}}^{i}=0.$$
We also note that Proposition 4 is only applicable to topologies with pair-wise sharing transmitters only, i.e., any transmitter can cover at most two receivers. Furthermore, the rate region for all the receivers are specified by the tunable values [TeX:] $$t_{i p}^{i}$$ such that the conditions in Proposition 4 are satisfied for all i and p. The larger [TeX:] $$t_{i p}^{i}$$ will allow the receiver [TeX:] $$R_{i}$$ to obtain a larger rate at the expense of a reduced rate for [TeX:] $$R_{p}.$$
Proposition 4 states that [TeX:] $$R_{i}$$ can be allocated [TeX:] $$t_{i p}^{i}$$ transmitters from [TeX:] $$t_{i p}$$ sharing transmitters between [TeX:] $$R_{i} \text { and } R_{p}$$ if:
Therefore, by applying Proposition 4 to all receivers [TeX:] $$R_{1}, R_{2}, \cdots, R_{n},$$ we can find suitable rates for all receivers in a given topology. The proof of Proposition 4 is shown below.
Proof. The proof is based on induction. The basis case of two receiver topology (n = 2) is true from Proposition 3. Now, suppose that Proposition 4 holds for n - 1 receiver topology, we will show that Proposition 4 will also hold for n receiver topology where one more receiver [TeX:] $$R_{n}$$ is added to the topology. Fig. 7 illustrates the inductive method.
First, using Proposition 4 with n - 1 receivers topology, receiver [TeX:] $$R_{i} \text { with } i \in\{1, \cdots, n-1\}$$ can achieve the rate:
It means that receiver [TeX:] $$R_{i}$$ is able to distinguish all value in set [TeX:] $$\left\{0,1, \cdots, c_{i}^{n-1}-1\right\}.$$ After adding receiver [TeX:] $$R_{n} \text { with } t_{n}$$ exclusive transmitters into network and [TeX:] $$t_{\text {in }}(i=1,2, \cdots, n-1)$$ sharing transmitters, for Proposition 4 to hold, we need to verify two following conditions:
Condition (a): All previous receivers [TeX:] $$R_{i} \text { with } i \in\{1, \cdots, \mathrm{n}- \ 1\}$$ can obtain additional [TeX:] $$t_{i n}^{i}$$ states, and therefore achieve the new rates:
Hence,
To do so, we need to verify that [TeX:] $$R_{i}$$ is able to distinguish all values in the set [TeX:] $$\left\{0,1, \cdots, c_{i}^{n}-1\right\}.$$
Condition (b): The new receiver [TeX:] $$R_{n}$$ also satisfies Proposition 4, i.e., [TeX:] $$R_{n}$$ is able to achieve the rate:
We first verify condition (a). Suppose that we need to transmit signal [TeX:] $$b_{i} \text { to } R_{i},$$ with:
Let us divide [TeX:] $$b_{i}$$ into two subsets:
· If [TeX:] $$0 \leq b_{i} \leq c_{i}^{n-1}-1$$ We will transmit [TeX:] $$b_{i}$$ in the n - 1 previous receiver topology (using the previous transmitters) and sends “0” using [TeX:] $$t_{i n}$$ sharing transmitters with new receiver [TeX:] $$R_{n}.$$ Clearly, [TeX:] $$R_{i}$$ will receive correct pattern since by assumption, Proposition 4 holds true for n - 1 receiver topology.
· If [TeX:] $$c_{i}^{n-1}-1<b_{i} \leq c_{i}^{n}-1 : $$ We will transmit signal [TeX:] $$c_{i}^{n-1}-1$$ in the n - 1 previous receiver topology and send the signal:
using the new [TeX:] $$t_{i n}$$ sharing transmitters. Clearly,
(20)
[TeX:] $$\begin{aligned} x_{i n} &=b_{i}-\left(c_{i}^{n-1}-1\right) \\ & \leq\left(c_{i}^{n}-1\right)-\left(c_{i}^{n-1}-1\right) \\ &=t_{i n}^{i} \end{aligned}$$
With (20) is due to (19), and:
(22)
[TeX:] $$\begin{aligned} x_{i n} &=b_{i}-\left(c_{i}^{n-1}-1\right) \\ & \geq\left(c_{i}^{n-1}-1\right)-\left(c_{i}^{n-1}-1\right) \\ &=0. \end{aligned}$$From (21) and (22): [TeX:] $$0 \leq x_{i n} \leq t_{i n}^{i} \leq t_{i n}, \text { then } t_{i n}^{i}$$ sharing transmitters can always transmit the signal [TeX:] $$x_{i n}.$$ Consequently, the received signal at[TeX:] $$R_{i} \text { is } y_{i}=c_{i}^{n-1}-1+x_{i n}$$ (note that [TeX:] $$c_{i}^{n-1}-1$$ comes from the transmitters in previous topology). Using the same decoding method as in (11), we have:
Therefore, the previous receiver [TeX:] $$R_{i}$$ can distinguish all values of [TeX:] $$b_{i} \in\left\{0,1, \cdots, c_{i}^{n}-1\right\}$$ and achieve the rate [TeX:] $$\log \left(c_{i}^{n}\right)$$ with:
(27)
[TeX:] $$\log \left(c_{i}^{n}\right)=\log \left(t_{i}+\sum_{p \neq i ; p=1}^{p=n} t_{i p}^{i}+1\right).$$Next, we verify condition (b) that the new receiver [TeX:] $$R_{n}$$ also satisfies Proposition 4, i.e., [TeX:] $$R_{n}$$ is able to achieve the rate:
Indeed, for a fixed pattern [TeX:] $$b_{i}$$ with [TeX:] $$i=1, \cdots, n-1$$ in the n-1 old receivers, we will prove that [TeX:] $$R_{n}$$ can discern [TeX:] $$c_{n}^{n}$$ states:
Consider [TeX:] $$R_{i}$$ with fixed pattern [TeX:] $$b_{i}$$ as in Fig. 7. We note that, of the [TeX:] $$t_{i n}$$ sharing transmitters between [TeX:] $$R_{i} \text { and } R_{n}, t_{i n}^{i}$$ transmitters are allocated to [TeX:] $$R_{i} \text { and } t_{i n}^{n}$$ remaining transmitters will be distributed to [TeX:] $$R_{n}.$$ Now, we can maintain the pattern [TeX:] $$b_{i}$$ by transmitting the pattern [TeX:] $$\left(b_{i}-\delta_{i}\right)$$ mod [TeX:] $$c_{i}^{n} \text { for } \forall i \in(1,2, \cdots, n-1)$$ using the transmission method as described in condition (a), then transmit pattern [TeX:] $$\delta_{i} \text { in } t_{i n}^{n}$$ remaining transmitters, where:
since the number of levels in [TeX:] $$\delta_{i}$$ cannot exceed the number of transmitters.
Now, from condition (18) in Proposition 4 for other pairwise sharing transmitter between [TeX:] $$R_{n} \text { and } R_{i},$$ we have:
Therefore,
The inequality above shows that [TeX:] $$R_{n}$$ is able to achieve [TeX:] $$\left(t_{i n}^{n}+1\right)$$ distinguishable states in pairwise sharing transmitter between [TeX:] $$R_{i} \text { and } R_{n}$$ when:
Thus, for all shared transmitters between [TeX:] $$R_{1}, R_{2}, \cdots, R_{n-1}$$ with [TeX:] $$R_{n} \text { and } t_{n}$$ exclusive transmitters of [TeX:] $$R_{n},$$ the number of distinguishable levels at [TeX:] $$R_{n}$$ is:
by additive property. Therefore, the achievable rate for [TeX:] $$R_{n}$$ is:
(28)
[TeX:] $$\log \left(c_{n}^{n}\right)=\log \left(t_{n}+\sum_{p=1}^{p=n-1} t_{n p}^{n}+1\right).$$In practice, there are many deployments that are not pairwise sharing topologies. We have a simple following result regarding the multi-user capacities:
Proposition 5: Given an arbitrary topology with k transmitters and n receivers [TeX:] $$R_{1}, R_{2}, \cdots, R_{n}.$$ If each receiver [TeX:] $$R_{i}$$ has an achievable rate [TeX:] $$\log \left(c_{i}^{n}\right)$$ bits per time slot, then
Proof. Since the maximum bit rate can be obtained using all k transmitters is k bits per second. This total rate must be shared among all the receivers. Thus, the proof follows.
General Topology. Proposition 5 is less useful since the described achievable rate region does not exploit the topological information. In what follows, we describe a very simple algorithm for converting many non-pairwise sharing topologies into
a pair-wise sharing topology whose achievable rate region can be characterized. In particular, a general topology consisting of k transmitters and n receivers can be characterized by collection of sets of different types of transmitters: exclusive transmitters, pairwise sharing transmitters, 3-sharing transmitters,[TeX:] $$\cdots, n -$$ sharing transmitters.
Initially, we construct a pairwise sharing topology that is characterized by all the exclusive and pairwise sharing transmitters from the set of all transmitters. If the condition in Proposition 4 is satisfied, then the achievable region for this pairwise sharing topology can be characterized. Now, the achievable region for a new topology that includes the existing pair-wise sharing topology and one additional m-sharing transmitter (m > 2) can be created as follows. Suppose this new transmitter is shared among [TeX:] $$R_{1}, R_{2}, \cdots, R_{m}$$ receivers. Then we can assign this new transmitter to a pair of receivers in [TeX:] $$\left(R_{1}, R_{2}, \cdots, R_{m}\right).$$ Suppose [TeX:] $$R_{i} \text { and } R_{j}$$ were chosen, then the number of shared transmitters for this pair [TeX:] $$t_{R_{i}} R_{j}$$ is increased by one. Effectively, we have a new pairwise sharing topology.
However since a transmission by the new shared transmitter will affect [TeX:] $$R_{1}, R_{2}, \cdots, R_{m},$$ we need to modify the encoding procedure slightly. First, if the new transmitter [TeX:] $$t_{R_{i} R_{j}}$$ transmits bit “0”, the encoding procedure for the bit pattern [TeX:] $$b_{i}$$ intended for [TeX:] $$R_{i}$$ is the same as one used for the pair-wise sharing topology without the new shared transmitter. This is because the bit “0” does not interfere with other signals. If [TeX:] $$t_{R_{i} R_{j}}$$ transmits bit “1”, then to transmit the original bit pattern [TeX:] $$b_{l}$$ intended for [TeX:] $$R_{l}, l \neq i, j$$ we encode [TeX:] $$b_{l}-1$$ instead using the same encoding procedure for the pair-wise sharing topology without [TeX:] $$t_{R_{i} R_{j}}.$$ Similar to the proof for Proposition 4, one sees that all [TeX:] $$R_{l}, l \neq i, j$$ will be able to recover original bit pattern [TeX:] $$b_{l}.$$ Specifically, either [TeX:] $$R_{i}$$ or [TeX:] $$R_{j}$$ will increase its capacity to [TeX:] $$\log \left(c_{i}+1\right) \text { or } \log \left(c_{j}+1\right),$$ depending on whether [TeX:] $$t_{R_{i} R_{j}}$$ is assigned to [TeX:] $$R_{i} \text { or } R_{j},$$ while other receivers will have the same capacities as before.
Maximum Sum Rate. is repeated and the corresponding achievable regions can be characterized if the conditions in Proposition 4 are satisfied. We also note that there are exponential large number of ways that the shared transmitters can be assigned to receivers, but the number of valid assignments based on Proposition 4, are generally a lot smaller. On the other hand, to maximize the sum rate of all the receivers, we have a greedy algorithm for determining which receiver should get a
new shared transmitter during the allocation. Specifically, we will allocate the shared transmitter to the receiver with smallest rate at every step for the following reason.
If we allocate a shared transmitter [TeX:] $$t_{R_{i} R_{j}} \text { to } R_{i}$$ which currently has an achievable rate [TeX:] $$\log \left(c_{i}\right),$$ then the capacity gain for [TeX:] $$R_{i}$$ is:
Similarly if we allocate a shared transmitter [TeX:] $$t_{R_{i} R_{j}} \text { to } R_{j},$$ then the capacity gain for [TeX:] $$R_{j}$$ is:
Clearly, [TeX:] $$\log \left(1+1 / c_{i}\right) \geq \log \left(1+1 / c_{j}\right) \text { if } c_{i} \leq c_{j}.$$ So, we should allocate the shared transmitter to the receiver with the smallest capacity currently if we want largest gain in one step (greedy) in capacity.
Multiple receivers in the same overlapped area: We note that a real-world topology may consist of multiple users in the same overlapped area. In this situation, we can treat these users as a superuser. Next, the proposed coding schemes can be applied to this superuser. Finally, a simple scheme such as time sharing (TDMA) can be applied to distribute the rate for multiple users in this overlapped area. For example, if the total rate for the superuser is 1 bit per time slot and there are two users inside the same overlapped area, one user will receive a bit per time slot while other achieves 1 - a bit per time slot where [TeX:] $$0 \leq a \leq 1,$$ depending on how we want to proportionally allocate the rates for the users, but the encoding/decoding procedure is identical for these users. In fact, this is the encoding and decoding procedures in Proposition 5 that aims to characterize the achievable rate region for general topology.
Example V.2: This example illustrates the procedure for converting a non-pair-wise sharing topology to pair-wise sharing topology and obtain a point in the achievable rate region. Fig. 8(a) represents a non-pairwise sharing topology with [TeX:] $$t_{1}= \ 1, t_{2}=1, t_{3}=2, t_{12}=t_{23}=t_{13}=2, \text { and } t_{123}=1.$$ Suppose we allocate [TeX:] $$t_{123}$$ to the pair [TeX:] $$\left(R_{1}, R_{3}\right).$$ Applying the aforementioned conversion procedure, we obtain the resulted pair-wise topology shown in Fig. 8(b) with:
Now we have a choice of selecting value for [TeX:] $$t_{13}^{1} \text { and } t_{13}^{3}{ }^{\prime}.$$ However, based on Proposition 4, the following constraints must hold:
All the pairs of [TeX:] $$\left(t_{12}^{1}, t_{12}^{2}, t_{23}^{2} t_{23}^{3}, t_{13}^{1}{ }^{\prime}, t_{13}^{3}{ }^{\prime}\right)$$ that can satisfy the above constraints are valid for receivers [TeX:] $$\left(R_{1}, R_{2}, R_{3}\right).$$ For example, the pairs [TeX:] $$t_{12}^{1}=1, t_{12}^{2}=1, t_{13}^{1}=2, t_{13}^{3}{ }^{\prime}=1, t_{23}^{2}=1, \ t_{23}^{3}=1$$ are valid. Hence, [TeX:] $$R_{1}, R_{2} \text { and } R_{3}$$ can achieve the rate [TeX:] $$\log (5), \log (4) \text { and } \log (5)$$ bit per time slot, respectively.
For example, suppose that we want to transmit the pattern [TeX:] $$\left(b_{1}=2, b_{2}=3, b_{3}=5\right) \text { to }\left(R_{1}, R_{2}, R_{3}\right),$$ respectively. Based on the conversion procedure discussion, there are two cases to consider: [TeX:] $$x_{123}=0 \text { and } x_{123}=1.$$
· Suppose [TeX:] $$x_{123}=0,$$ then based on the encoding in the conversion procedure, the pattern [TeX:] $$\left(b_{1}=2, b_{2}=3, b_{3}=5\right)$$ is transmitted normally. Using Proposition 4, we construct n = 3 sets according the encoding procedure:
Next, a set of feasible solution to the above inequalities is:
Now, we note that the decoding procedure sums up all the signal at the receiver:
As seen, they are all correct.
· Suppose [TeX:] $$x_{123}=1.$$ Then based on the encoding in the conversion procedure, the pattern [TeX:] $$\left(b_{1}=1, b_{2}=2, b_{3}=4\right)$$ is transmitted. Using Proposition 4, we construct n = 3 sets based
Fig. 9.
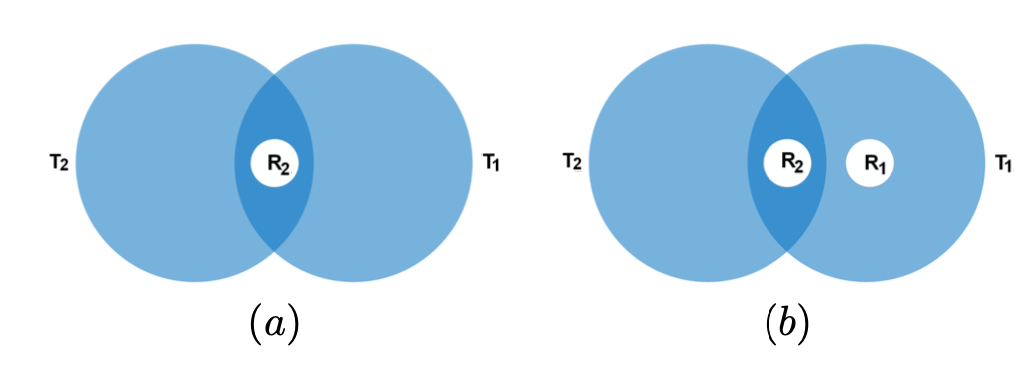
Fig. 10.
on the encoding procedure:
Next, a set of feasible solution to the inequality above is:
Now, the decoding procedure sums up all the signal go to receiver:
to correctly reconstruct the transmitted patterns.
Fig. 11.
D. Achievable rate Region for ideal channels
This section shows how LAC cooperative transmission techniques SRC, ERC, and JRC are used to characterize the achievable rate regions for real-world topologies.
D.1 Achievable Rate Region for Two-Transmitter Topologies
For the two-transmitter topologies with the number of receivers being smaller than the number of transmitters, there are only two canonical topologies shown in Fig. 9. Other topologies where receivers are not in an overlapped region are trivial.
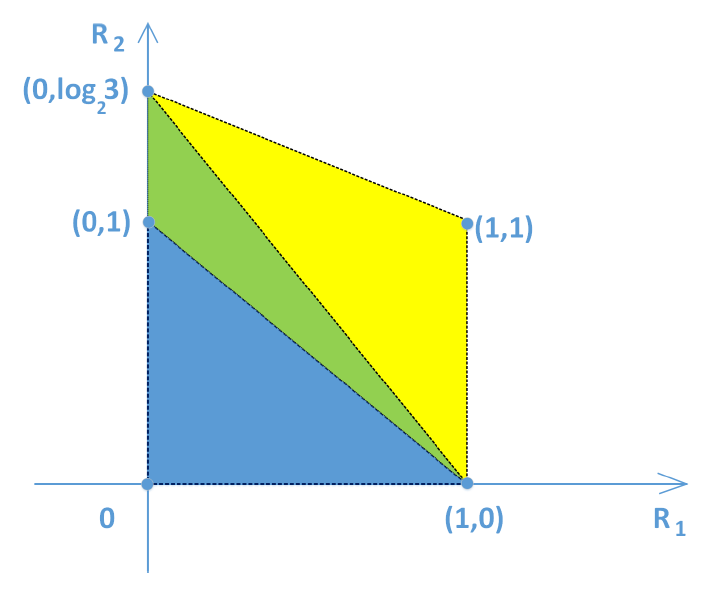
Using time-sharing scheme between [TeX:] $$R_{1} \text { and } R_{2},$$ the achievable rate region is depicted as the blue triangle in Fig. 11 with its boundary being a linear interpolation of two achievable rate tuples (0, 1) and (1, 0). Now, using SRC (Proposition 1) for [TeX:] $$R_{2} \text { and } R_{1},$$ rate tuples (0, log 3) and (1, 0) are achievable. Thus, SRC helps enlarge the achievable region by additional green area. The achievable region can be further enlarged by an additional yellow area by using SRC for [TeX:] $$R_{2}$$ to obtain the rate tuple (0; log 3) and ERC (Proposition 2) for both [TeX:] $$R_{1} \text { and } R_{2}$$ to obtain the rate tuple (1, 1). Consequently, the achievable rate region is obtained by interpolation between the two rate tuples (0; log 3) and (1, 1).
D.2 Achievable Rate Region for Three-Transmitter Topologies
Similar to the two-transmitter topologies, the achievable rate region of the three-transmitter topologies is constructed by finding the feasible tuples that can be achieved using SRC and ERC, and additionally JRC. The convex hull of these feasible tuples
Fig. 13.
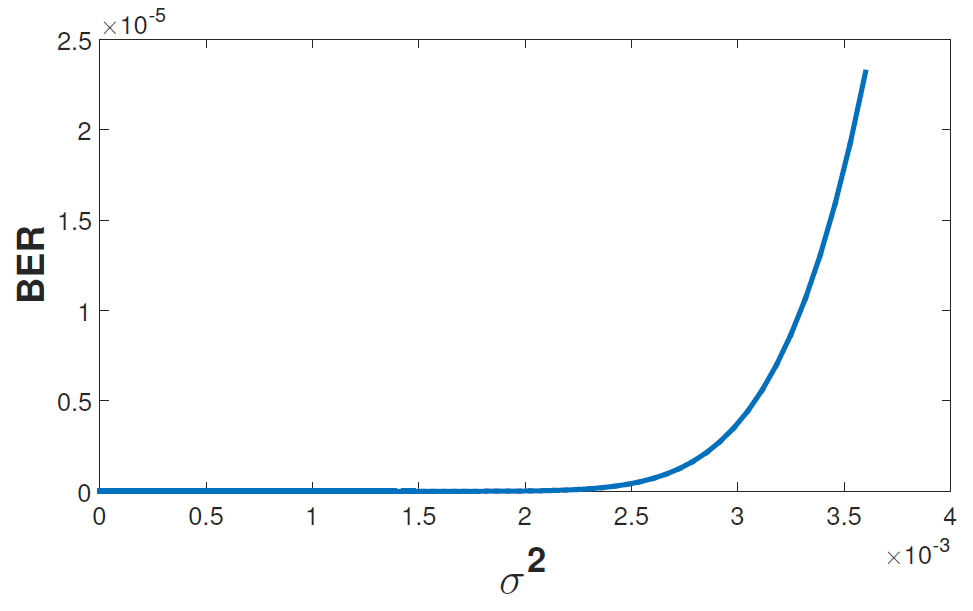
Fig. 14.
is the achievable rate region. Specifically, for three-transmitter topologies, the canonical topologies with the number receivers: 1, 2, and 3, are as shown in Fig. 10. First, using SRC (Proposition 1) for [TeX:] $$R_{3}, R_{2} \text { and } R_{1},$$ rate tuples (0, 2, 0), (log 3, 0; 0) and (0, 0, 1) are achievable. Note that the x; y, and z coordinates denote the rate for [TeX:] $$R_{2}, R_{3}, \text { and } R_{1} \text {, }$$ respectively. Next, using ERC (Proposition 2), the feasible tuple (1,1,1) can be obtained. Next, by applying JRC (Proposition 3) for topologies in Fig. 10(c) and 10(d), the two tuples (log 3, 1, 0) and (0, log 3, 1) can be obtained, respectively. Specifically, for the tuple (0, log 3, 1), the number of exclusive transmitters for [TeX:] $$R_{1}$$ and [TeX:] $$R_{3} \text { are } t_{1}=0 \text { and } t_{3}=2$$ while the number of shared transmitters [TeX:] $$t_{13}=1.$$ Using Proposition 3 with [TeX:] $$t_{13}^{1}=1 \text { and } t_{13}^{3}=0,$$ the achievable rate of [TeX:] $$R_{1} \text { is } \log \left(t_{1}+t_{13}^{1}+1\right)=1,$$ and for [TeX:] $$R_{3}, \ \log \left(t_{3}+t_{13}^{3}+1\right)=\log (3).$$ Using the same technique for [TeX:] $$R_{3}$$ and [TeX:] $$R_{2}$$ shown in Fig. 10(c), the feasible tuple (log 3, 1, 0) can be obtained.
Finally, Fig. 12 shows the overall achievable rate region as a convex hull of the feasible tuples: (0, log 3, 1), (log 3, 1, 0), (1, 1, 1), (0, 0, 1), (log 3, 0, 0), (0, 2, 0).
D.3 Simulation Results
To provide some insights to the performance of LAC in practical settings, we provide simulation results for the bit error rates of using LAC under AWGN channels. Our simulation uses the channel model where two transmitters send data to two receivers as shown in Fig. 3. Each transmitter can send a signal corre sponding to one of two levels “0” and “1”. Thus, the received signals at the receiver [TeX:] $$R_{j}$$ is
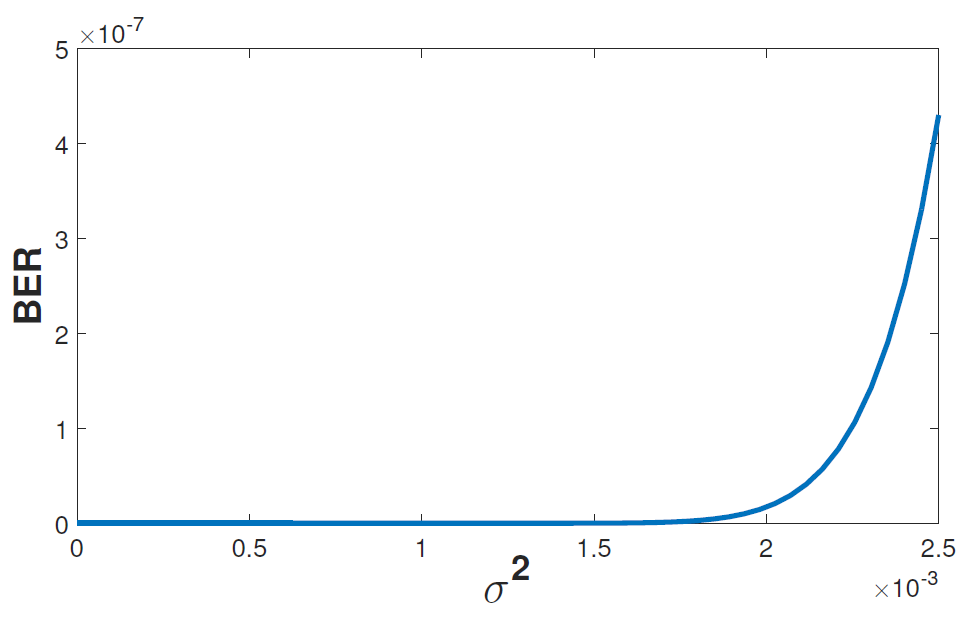
where [TeX:] $$x_{i}$$ is the transmitted signal from transmitter [TeX:] $$T_{i}, \alpha_{i j}$$ is the attenuation factor from transmitter [TeX:] $$T_{i}$$ to receiver [TeX:] $$R_{j}, \text { and } n_{j}$$ is the additive noise at receiver [TeX:] $$R_{j}.$$ To decode the received signal [TeX:] $$y_{j}$$ back to “0” or “1”, the receiver uses a threshold h. The method for determining the optimal h can be found in [33]. Using attenuation factors [TeX:] $$\alpha_{12}=0.6 \text { and } \alpha_{22}=0.9,$$ Fig. 13 and 14 show the bit error rate of [TeX:] $$R_{2}$$ vs. the variance of additive Gaussian noise without and with FEC, respectively. As seen, the bit error rate increases if the variance of the noise increases. Furthermore, the bit error rate is reduced significantly from [TeX:] $$10^{-5}$$ to [TeX:] $$10^{-7}$$ when FEC is employed.
VI. CONCLUSION
In this paper, we describe a coding scheme for FSO communications called LAC that uses location information to improve the capacity of the receivers in a dense deployment topology. Depending on the topology matrix, three coding/decoding schemes are proposed to help increase throughput and reduce interference for multiple users in a dense array of overlapped femtocells. Using this coding schemes, the multi-user achievable rate region is characterized. Both numerical and theoretical results are provided to justify the proposed coding techniques.
Biography
Thuan Nguyen
Thuan Nguyen received a B.S. degree in Electrical Engineering (honors program) from Post and Telecommunication Institute of Technology, Vietnam, in 2013 and the M.S. and Ph.D. degrees in Electrical Computer Engineering from Oregon State University in 2018 and 2021, respectively. His research interests include information theory, signal processing and machine learning. He is currently a Postdoc Researcher at Tufts University, Boston, MA, USA.
Biography
Duong Nguyen-Huu
Duong Nguyen-Huu received the B.S. degree from the Hanoi University of Technology in 2009, and the M.S. and Ph.D. degrees in Computer Engineering from Oregon State University in 2013 and 2016, respectively. He is currently a Software Engineer at Microsoft. His research interests are network coding, stochastic optimization, cloud computing, and networking applications.
Biography
Thinh Nguyen
Thinh Nguyen received the B.S. degree from the University of Washington, Seattle, WA, USA, in 1995 and the Ph.D. degree from the University of California, Berkeley, CA, USA, in 2003, both in Electrical Engineering. He is currently a Professor with the School of Electrical Engineering and Computer Science, Oregon State University, Corvallis, OR, USA. He is interested in all things stochastic, with applications to signal processing, distributed systems, wireless networks, network coding, and quantum walks. Dr. Nguyen has
References
- 1 Q. Wang, T. Nguyen, A. X. Wang, "Channel capacity optimization for an integrated wi-fi and free-space optic communication system (wififo)," in Proc.ACMMSWIM, 2014.custom:[[[-]]]
- 2 S. T. Liverman, Q. Wang, Y.-J. Chu, A. Natarajan, T. Nguyen, A. X. Wang, "Hybrid wireless communication networks: Integrating free-space optics and wifi," FrontiersinOptics2016p. JTh2A.56, 2016.custom:[[[-]]]
- 3 T. Nguyen, D. Nguyen-Huu, T. Nguyen, "On achievable rate region using location assisted coding (lac) for fso communication," in Proc.IEEE VTC-Fall, 2017.custom:[[[-]]]
- 4 T. Duong, D. Nguyen-Huu, T. Nguyen, "Location assisted coding (lac): Embracing interference in free space optical communications," in Proc.ACMQ2SWinet, 2015.custom:[[[-]]]
- 5 M. Najafi, V. Jamali, R. Schober, "Adaptive relay selection protocol for the parallel hybrid rf/fso relay channel," in Proc.IEEE ICC, 2016.custom:[[[-]]]
- 6 L. Chen, W. Wang, C. Zhang, "Multiuser diversity over parallel and hybrid fso/rf links and its performance analysis," IEEE PhotonicsJ., vol. 8, no. 3, pp. 1-9, 2016.custom:[[[-]]]
- 7 V. Jamali, D. S. Michalopoulos, M. Uysal, R. Schober, "Link allocation for multiuser systems with hybrid rf/fso backhaul: Delay-limited and delay-tolerant designs," IEEE Trans.WirelessCommun., vol. 15, no. 5, pp. 3281-3295, 2016.custom:[[[-]]]
- 8 A. Douik, H. Dahrouj, T. Y. Al-Naffouri, M.-S. Alouini, "Hybrid radio/free-space optical design for next generation backhaul systems," IEEE Trans.Commun., vol. 64, no. 6, pp. 2563-2577, 2016.custom:[[[-]]]
- 9 H. Haas, L. Yin, Y. Wang, C. Chen, "What is lifi?," J. Lightwave Technol., vol. 34, no. 6, pp. 1533-1544, 2016.custom:[[[-]]]
- 10 B. Patnaik, P. Sahu, "Design and study of high bit-rate free-space optical communication system employing qpsk modulation," Int.J.Signal ImagingSyst.Eng., vol. 6, no. 1, pp. 3-8, 2013.custom:[[[-]]]
- 11 N. Cvijetic, D. Qian, T. Wang, "10gb/s free-space optical transmission using ofdm," in Proc.OFC, 2008.custom:[[[-]]]
- 12 L. A. Kadhim, "16/64qam modulation technique for free space optical communication system," Int. J. Advancements Comput. Technol.p. 1, vol. 6, no. 6, 2014.custom:[[[-]]]
- 13 I. B. Djordjevic, B. Vasic, M. A. Neifeld, "Multilevel coding in freespace optical mimo transmission with q-ary ppm over the atmospheric turbulence channel," IEEE Photon.Technol.Lett.p. 1491, vol. 18, no. 13/16, 2006.custom:[[[-]]]
- 14 T. T. Nguyen, L. Lampe, "Coded multipulse pulse-position modulation for free-space optical communications," IEEE Trans. Commun., vol. 58, no. 4, pp. 1036-1041, 2010.custom:[[[-]]]
- 15 A. Sevincer, A. Bhattarai, M. Bilgi, M. Yuksel, N. Pala, "Lightnets: Smart lighting and mobile optical wireless networks—a survey," IEEE Commun.SurveysTuts., vol. 15, no. 4, pp. 1620-1641. custom:[[[-]]]
- 16 H. Henniger, O. Wilfert, "An introduction to free-space optical communications," RADIOENGINEERINGp. 203, vol. 19, no. 2, 2010.custom:[[[-]]]
- 17 D. G. M. John R. Barry, E. A. Lee, AnIntroductiontoFree-spaceOpticalCommunications. Norwell, MA, USA: Kluwer Academic Publishers, 2003.custom:[[[-]]]
- 18 A. Goldsmith, S. A. Jafar, N. Jindal, S. Vishwanath, "Capacity limits of mimo channels," IEEE J. Sel. Areas Commun., vol. 21, no. 5, pp. 684-702, 2003.custom:[[[-]]]
- 19 E. Björnson, E. G. Larsson, T. L. Marzetta, "Massive mimo: Ten myths and one critical question," IEEE Commun. Mag., vol. 54, no. 2, pp. 114-123, 2016.custom:[[[-]]]
- 20 E. G. Larsson, O. Edfors, F. Tufvesson, T. L. Marzetta, "Massive mimo for next generation wireless systems," IEEE Commun.Mag., vol. 52, no. 2, pp. 186-195, 2014.custom:[[[-]]]
- 21 G. J. Foschini, M. J. Gans, "On limits of wireless communications in a fading environment when using multiple antennas," Wireless Personal Commun., vol. 6, no. 3, pp. 311-335, 1998.custom:[[[-]]]
- 22 T. Nguyen, T. Nguyen, "Embedded coding techniques for fso communication," in Proc.IEEE VTC-Fall, 2017.custom:[[[-]]]
- 23 D. Gesbert, M. Shafi, D.-s. Shiu, P. J. Smith, A. Naguib, "From theory to practice: an overview of mimo space-time coded wireless systems," IEEE J.Sel.AreasCommun., vol. 21, no. 3, pp. 281-302, 2003.custom:[[[-]]]
- 24 L. Poo, "Space-time coding for wireless communication: A survey," Report from Standford University, 2002.custom:[[[-]]]
- 25 T. M. Cover, "Broadcast channels," IEEE Trans.Inf.Theory, vol. 18, no. 1, pp. 2-14, 1972.custom:[[[-]]]
- 26 R. G. Gallager, "Capacity and coding for degraded broadcast channels," ProblemyPeredachiInformatsii, vol. 10, no. 3, pp. 3-14, 1974.custom:[[[-]]]
- 27 T. Nguyen, T. Nguyen, "Achievable rate regions for location assisted coding (lac)," TechnicalReportOregonStateUniversity, June, 2016.custom:[[[-]]]
- 28 K. Marton, "A coding theorem for the discrete memoryless broadcast channel," IEEE Trans.Inf.Theory, vol. 25, no. 3, pp. 306-311, Sept, 2006.custom:[[[-]]]
- 29 S. Katti, H. Rahul, W. Hu, D. Katabi, M. Médard, J. Crowcroft, "Xors in the air: Practical wireless network coding," ACMSIGCOMMcomputer commun.review, vol. 36, no. 4, pp. 243-254, 2006.custom:[[[-]]]
- 30 S. Agnihotri, S. Jaggi, M. Chen, "Analog network coding in general snr regime: performance of a greedy scheme," in Proc.NetCod, 2012.custom:[[[-]]]
- 31 S. Liverman, Q. Wang, Y.-J. Chu, A. Borah, S. Wang, A. Natarajan, A. X. Wang, T. Nguyen, "Wifo: A hybrid communication network based on integrated free-space optical and wifi femtocells," ComputerCommun., vol. 132, pp. 74-83, 2018.custom:[[[-]]]
- 32 T. M. Cover, J. A. Thomas, Elements of Information Theory(Wiley Series in Telecommunications and Signal Processing). Wiley-Interscience, 2006, 2006.custom:[[[-]]]
- 33 Y.-J. Chu, T. Nguyen, Z. N. Stark, "Wifo: Hybrid wifi and free-space optical communication system with pam optimal decoding," in Proc.IEEE ICCCN, 2016.custom:[[[-]]]







