Emily Jimin Roh , Soohyun Park , Soyi Jung and Joongheon Kim
Stabilized Classification Control using Multi-Stage Quantum Convolutional Neural Networks for Autonomous Driving
Abstract: Real-time processing with high classification accuracy is a fundamental requirement in autonomous driving systems. However, existing neural network models for classification often face a tradeoff between computational efficiency and accuracy, necessitating the development of advanced optimization methods to address this limitation. Additionally, dynamic driving environments offer opportunities to enhance classification performance by leveraging the principles of quantum computing, particularly the properties of superposition and entanglement. In response to these challenges, a multi-stage quantum convolutional neural network (MS-QCNN) approach is proposed, designed to improve image analysis performance by effectively utilizing the multi-stage structure of QCNN. A Lyapunov optimization framework is applied to achieve optimal performance, which maximizes time-averaged efficiency while ensuring system stability. This framework dynamically adjusts the MS-QCNN model in response to environmental variations, promoting enhanced queue stability and achieving optimal time-averaged performance.
Keywords: Autonomous driving , Lyapunov optimization , multi-stage quantum convolutional neural network
I. INTRODUCTION
IN the rapidly evolving domain of autonomous driving, ensuring real-time data processing with high classification accuracy is critical [1], [2]. Consistently stabilized classification accuracy is a foundational element, enabling autonomous vehicles to accurately perceive and interpret their environments for critical tasks such as obstacle detection, lane identification, and traffic sign recognition [3]. The effectiveness of these systems is heavily dependent on their ability to balance computational efficiency with classification accuracy, a tradeoff that has posed significant challenges for existing neural network architectures [4]. As autonomous driving scenarios become increasingly complex, there is a growing need for innovative approaches that address this limitation while maintaining robustness and reliability.
While effective in static environments, conventional neural network models often fail to meet the stringent demands of real-time, dynamic systems like autonomous vehicles [5]. The computational cost of achieving high accuracy can become prohibitive, mainly when real-time processing constraints are considered [6]. To address this challenge, efforts have focused on exploring optimization techniques to improve the performance of neural networks without significantly increasing their computational overhead [7]. Despite these efforts, existing approaches struggle to fully exploit the potential for adaptive and efficient processing in rapidly changing environments, necessitating new paradigms for improvement [8].
Recent advancements in quantum computing have introduced a new dimension to addressing these challenges [9]–[11]. Quantum principles such as superposition and entanglement offer unique opportunities for building more efficient computational models. Quantum convolutional neural networks (QCNNs), which utilize the quantum neural network in classical convolutional architectures, have emerged as a promising direction for enhancing real-time image analysis in autonomous systems [12]. QCNNs leverage the inherent parallelism of quantum computing to handle complex data structures more efficiently, making them well-suited for dynamic, real-world applications [13], [14].
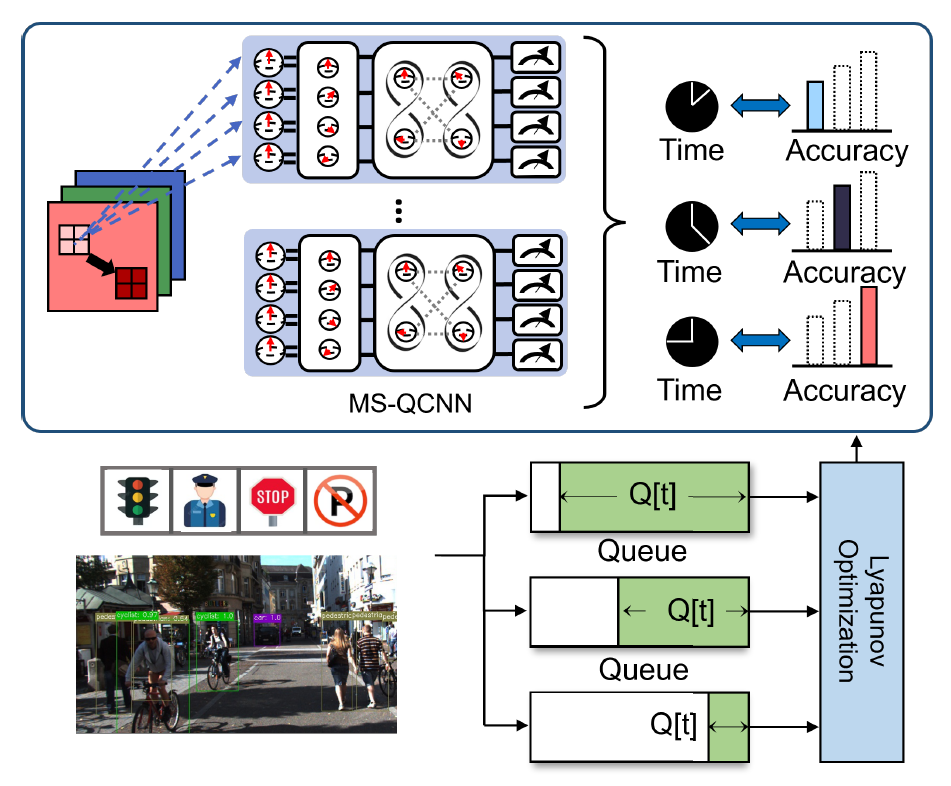
To further enhance the capabilities of QCNNs, a multistage quantum convolutional neural network (MS-QCNN) framework is proposed. The MS-QCNN approach incorporates a multi-stage structure designed to improve the accuracy and efficiency of image classification tasks. The overall architecture of the proposed stabilized classification control using MS-QCNN is illustrated in Fig. 1, providing a visual representation of the framework’s key components and their interactions. By adopting a Lyapunov optimization framework [15], [16], the proposed method ensures system stability while dynamically adjusting to environmental variations. This framework maximizes time-averaged computational efficiency, optimally balancing resource allocation and processing speed in response to changing conditions [17], [18]. Furthermore, the Lyapunov approach facilitates queue stability, ensuring consistent performance even under high-demand scenarios common in autonomous driving environments [19].
Therefore, this paper bridges the gap between classical neural networks and quantum-enhanced models, addressing the limitations of existing methods while opening new avenues for real-time data processing in autonomous systems. The proposed stabilized classification control using MS-QCNN framework aims to set a new benchmark for efficient, accurate, and adaptive classification in dynamic environments by integrating quantum computing principles with Lyapunov optimization.
Contributions. The main contributions of this paper are summarized as follows.
· First of all, this paper proposes the MS-QCNN architecture that adjusts the multi-stage of QCNN to enhance the accuracy and efficiency of real-time image classification in autonomous systems.
· Moreover, the proposed algorithm in this paper implements a Lyapunov optimization framework to adjust the MS-QCNN in response to environmental variations dynamically, ensuring system stability and maximizing time-averaged computational efficiency.
· Lastly this paper establishes a novel stabilized MS-QCNN control framework for efficient and accurate classification in autonomous systems by integrating quantum computing concepts with Lyapunov optimization, paving the way for future developments in the field.
Organization. The remainder of this paper is organized as follows. Section II introduces the main algorithms proposed in this work, including their design and theoretical underpinnings. Section III presents experimental results that highlight the robustness and effectiveness of the proposed stabilized MSQCNN control under varying conditions. Finally, Section IV concludes the paper by summarizing key findings and outlining potential directions for future research to advance this framework.
II. STABILIZED CLASSIFICATION CONTROL USING MS-QCNN FOR AUTONOMOUS DRIVING
The paper integrates the MS-QCNN with Lyapunov optimization to achieve stabilized classification performance in dynamic autonomous driving environments. The MS-QCNN model is designed to enhance classification accuracy and efficiency by leveraging the multi-layered structure of QCNNs. To ensure stability and adaptability, a Lyapunov optimizationbased control is employed, enabling dynamic adjustment of the MS-QCNN in response to environmental variations.
A. MS-QCNN Framework
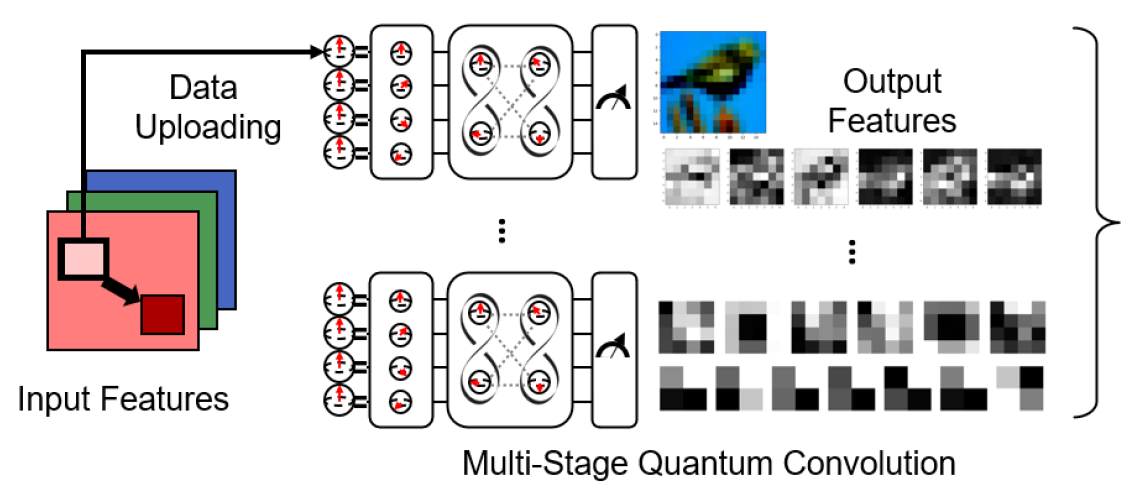
The MS-QCNN framework extends the functionality of the QCNN by introducing a multi-stage architecture that dynamically adjusts to varying environmental demands. This flexibility is achieved by controlling the depth and configuration of the QCNN layers, allowing the model to optimize its performance based on task complexity and computational constraints [20]. The architecture of MS-QCNN is illustrated in Fig. 2.
Fig. 2.
1) QCNN layer: For classification tasks, the Im2col operation, a common technique in CNN optimization, is employed [21]. The input tensor is defined as [TeX:] $$T \in \mathbb{R}^{K_{i n} \times H \times W}$$, where [TeX:] $$K_{i n}, H, \text { and } W$$ represent the number of input channels, height, and width of the tensor, respectively. The filter is specified as,
where [TeX:] $$K_o$$ is the number of output channels, and h and w are the height and width of the filter. To perform the convolution operation, padding p and stride s are applied to the input tensor T. The data pre-processing step transforms the input tensor T into a new tensor [TeX:] $$T^{\prime} \in \mathbb{R}^{\left(K_{i n} \times h \times w\right) \times\left(H_o \times W_o\right)}.$$ Here, the output height [TeX:] $$H_o$$ and width [TeX:] $$W_o$$ are computed as follows,
and, this transformation organizes the input tensor into a format that facilitates efficient convolution operations. To incorporate quantum computations, the channel data is uploaded into identical geometrical spaces using an q-qubit quantum circuit as,
(4)
[TeX:] $$|\psi\rangle_i=\prod_{\kappa=0}^{K_{i n}} \prod_{j=0}^{h_\kappa w_\kappa} R_{\varphi}\left(x_{\kappa, j}\right)|0\rangle^{\otimes q},$$where [TeX:] $$i \in \mathbb{N}\left[0, H_o \times W_o\right) \text { and } \varphi \in\{x, y, z\} .$$ In this context, [TeX:] $$R_{\varphi}\left(x_{\kappa, j}\right)$$ denotes a quantum rotation gate applied along the axis x, y and z, where the input value [TeX:] $$x_{\kappa, j}$$ determines the rotation angle. This gate enables the encoding of classical data into quantum states by rotating qubits accordingly, facilitating the representation of input features within the quantum circuit. Here, [TeX:] $$h_\kappa \text { and } w_\kappa$$ is the height and width of the [TeX:] $$\kappa \text {th}$$ channel, respectively. This approach encodes the ith row, representing a convolution operation, entirely into the quantum state [TeX:] $$|\psi\rangle_i$$ [22]. The ith quantum convolution is then expressed as,
where [TeX:] $$U_G(\theta)$$ is a set of trainable rotation and CNOT gates. In this paper, [TeX:] $$U_G(\theta)$$ is implemented using a U3CU3 layer, where U3 gates are applied for arbitrary single-qubit rotations and controlled-U3 gates are utilized to capture entanglement between qubits, enabling flexible and expressive quantum transformations within the convolutional layer. The transformed quantum state [TeX:] $$\left|\psi_\theta\right\rangle_i$$ must be decoded into a classical output to enable compatibility with classical computing systems. The expectation value, i.e.,
(6)
[TeX:] $$\left\langle O_{\mathbf{x}, \theta}\right\rangle=\prod_{M \in \mathcal{M}}\left\langle\psi_{\mathbf{x}, \theta}\right| M\left|\psi_{\mathbf{x}, \theta}\right\rangle,$$denotes the expectation of the transformed quantum state [TeX:] $$\left|\psi_{\mathbf{x}, \theta}\right\rangle$$ on the Hermitian M. This process produces outputs [TeX:] $$\left\langle O_{\mathrm{x}, \theta}\right\rangle \in[-1,1]^{\otimes q} .$$ For simplicity, the results are represented as,
(7)
[TeX:] $$\langle O\rangle \triangleq\left\langle O\left(\left|\psi_\theta\right\rangle_i\right)\right\rangle \mid i \in \mathbb{N}\left[0, H_{\mathrm{o}} \times W_{\mathrm{o}}\right] .$$Given the number of quantum convolutions [TeX:] $$i \in \mathbb{N}\left[0, H_{\mathrm{o}} \times W_{\mathrm{o}}\right],$$ the output dimension is expressed as [TeX:] $$\langle O\rangle \in \mathbb{R}^{\left(H_0 \times W_0\right) \times q} .$$ To harmonize the dimensions of classical data, the QCNN employs a fully connected network of size [TeX:] $$\left(q, K_{\mathrm{o}}\right)$$ to reconstruct the channel data, yielding [TeX:] $$\left(q, K_{\mathrm{o}}\right)$$ [TeX:] $$f_r(O) \in \mathbb{R}^{\left(H_0 \times W_0\right) \times K_0},$$ where [TeX:] $$f_r(\cdot)$$ denotes the channel reconstruction. By permuting the resulting tensor and treating q as the seed channels, the QCNN achieves functional equivalence with a classical CNN.
2) Multi-Stage architecture design: The MS-QCNN architecture, as detailed in Algorithm 1 enhances the functionality of the standard QCNN by introducing a hierarchical and multistage design. This design enables dynamic adaptability to task complexities and resource constraints, ensuring efficient feature extraction and robust classification performance. Each stage consists of one quantum convolutional layer, where quantum convolution operations are applied sequentially to the input quantum states. In each stage, the quantum convolutional operation applies a unitary transformation designed to extract meaningful patterns from the quantum state. Let the architecture consist of Γ stages, and the input to the [TeX:] $$\gamma \text{th}$$ stage be represented as [TeX:] $$T^\gamma.$$ The quantum convolution operation at the [TeX:] $$\gamma \text{th}$$ stage can be expressed as,
(8)
[TeX:] $$\left|\psi_{\mathbf{x}, \theta}^\gamma\right\rangle=U_G^\gamma\left(\theta^\gamma\right)\left|\psi_{\mathbf{x}, \theta}^{\gamma-1}\right\rangle,$$where [TeX:] $$\left|\psi_{\mathbf{x}, \theta}^{\gamma-1}\right\rangle$$ is the output state from the previous stage (or the input state for the first stage). [TeX:] $$U_G^\gamma\left(\theta^\gamma\right)$$ is the unitary transformation representing the quantum convolution operation, parameterized by [TeX:] $$\theta^\gamma$$. The convolution operation applies a localized transformation across subsets of qubits, analogous to classical convolution, enabling efficient feature extraction while preserving quantum information [21]. To transform the quantum state into classical output, Pauli-Z measurements are performed at each stage [23]. The expectation values are calculated over the quantum states processed through the convolution layers. The expectation value for the [TeX:] $$\gamma \text{th}$$ stage is defined as,
(9)
[TeX:] $$\left\langle O_{\mathbf{x}, \theta}^\gamma\right\rangle=\prod_{M \in \mathcal{M}^\gamma}\left\langle\psi_{\mathbf{x}, \theta}^\gamma\right| M\left|\psi_{\mathbf{x}, \theta}^\gamma\right\rangle .$$In this equation, [TeX:] $$\left\langle\psi_{\mathbf{x}, \theta}^\gamma\right| M\left|\psi_{\mathbf{x}, \theta}^\gamma\right\rangle$$ represents the expected measurement outcome for the quantum state at the [TeX:] $$\gamma \text{th}$$ stage, where the measurement operator M is applied to extract classical information from the quantum state, thereby enabling the assessment of quantum feature transformations. Here, [TeX:] $$\mathcal{M}^\gamma$$ is the measurement set specific to the [TeX:] $$\gamma \text{th}$$ stage, defined as,
Here, [TeX:] $$M_q^\gamma$$ specifies the measurement operator for the qth qubit, where the Pauli-Z operator Z is applied to the target qubit. The identity operator I is applied to the remaining qubits, ensuring that the measurement focuses on the intended qubits while preserving the quantum information of the others. Consequently, the decoding process ensures that the expectation values fall within the range [TeX:] $$\left\langle O_{\mathbf{x}, \theta}^\gamma\right\rangle \in[-1,1]^{\otimes q} .$$ The hierarchical structure of the MS-QCNN ensures that each stage progressively extracts higher-order features from the input quantum data. The convolutional layers capture localized quantum correlations, while decoding transforms these into classical probabilities. This allows the MS-QCNN to adapt dynamically to task-specific demands, balancing computational efficiency with classification accuracy.
B. Lyapunov Optimization-based MS-QCNN Selection
In autonomous driving systems, ensuring real-time classification of environmental data is crucial for navigation and safety [24]. To address the varying demands of computational resources, environmental dynamics, and accuracy requirements, a Lyapunov optimization framework is utilized to manage the adaptive adjustment of the MS-QCNN’s γ-parameter, which represents the number of stages in our MS-QCNN architecture, as detailed in Algorithm 2. By dynamically selecting γ, the framework balances computational efficiency and classification performance to meet system constraints in real-time [25].
1) Lyapunov optimization framework: The Lyapunov optimization framework captures delays and computational demands using a queue-based model, where the queuebacklog Q[t] represents the system state at time t [26]. This framework uses Lyapunov drifts to model queue dynamics, allowing real-time selection of the optimal γ value for the MSQCNN. This adaptive mechanism facilitates time-averaged, sequential decision-making for stage-level adjustment while guaranteeing queue stability and maintaining accuracy [27]. The queue dynamics are defined as,
where Q[t] is the queue-backlog size at time t, with Q[0] = 0. The term a[t] represents the arrival process, defined as the video frames received by the system per cycle, modeled as independent and identically distributed (i.i.d.) random events [28]. The service process [TeX:] $$b(\alpha[t])$$ is the system’s ability to process data at time t, which depends on the selected MSQCNN stage parameter [TeX:] $$\alpha[t]$$. A higher γ implies deeper feature extraction but increases computational load, whereas a lower γ reduces computation but may compromise classification accuracy. The arrival process a[t] is modeled as the ratio of frames per second (fps) processed relative to the default fps, given by,
where [TeX:] $$w_f$$ represents the default fps, and ζ[t] depends on the computational cost associated with the selected stage depth γ. The service process b(α[t]) depends on the computational cost associated with the selected stage depth γ as,
where [TeX:] $$\gamma \in\{1,2,3\}, \text { and } w_\gamma$$ represents the computational cost corresponding to the MS-QCNN configuration with γ stages, respectively. The range of [TeX:] $$\gamma \in\{1,2,3\}$$ was carefully determined based on both practical constraints and application requirements. Due to the limitations of the current noisy intermediate-scale quantum (NISQ) era, increasing γ beyond 3 stages is challenging, as it exceeds the feasible qubit capacity and computational resources available for simulation. Additionally, in the context of autonomous driving, where realtime processing is critical, keeping the model lightweight is essential to minimize inference time. Therefore, the selection of γ values up to 3 ensures a balanced tradeoff between computational efficiency and classification accuracy, aligning with both hardware constraints and application demands. This design choice reflects the need to maintain efficient real-time processing while considering the limitations of current quantum hardware. The classification accuracy [TeX:] $$\zeta(\alpha[t])$$ depends on the stage depth, γ, which determines the complexity of feature extraction. The Lyapunov optimization framework ensures that the system dynamically selects [TeX:] $$\alpha[t]$$ based on the current state Q[t] to balance computational efficiency and accuracy. The objective is to maximize time-averaged detection accuracy [TeX:] $$\zeta(\alpha[t])$$ while maintaining queue stability. The primary objective of the Lyapunov optimization framework for the MSQCNN selection process is,
In this equation, the term [TeX:] $$\sum_{\tau=0}^{t-1} \zeta(\alpha[\tau])$$ represents the cumulative classification accuracy over time, which plays a critical role in ensuring that the system consistently selects the optimal MS-QCNN configuration [TeX:] $$\alpha[\tau]$$ to enhance overall performance, thereby achieving a balance between immediate and long-term optimization goals. Therefore, this ensures that the system prioritizes maximizing classification accuracy in the long term, balancing short-term decisions against overall performance. To ensure that the system operates within practical limits, the Lyapunov optimization framework imposes a queue stability constraint,
In this equation, [TeX:] $$\lim _{t \rightarrow \infty} \frac{1}{t} \sum_{\tau=0}^{t-1} Q[\tau]$$ represents the time-averaged queue backlog, which plays a critical role in ensuring system stability by preventing the backlog from growing indefinitely, thereby guaranteeing that the average delay in processing incoming data remains within practical and acceptable limits. Therefore, this constraint ensures that the queue backlog remains finite, avoiding system overload and guaranteeing timely processing of incoming data streams [29]. Without this constraint, the queue backlog could grow indefinitely, leading to delays and degraded system performance [30]. By integrating these objectives, the framework ensures that the system dynamically selects the optimal MS-QCNN configuration [TeX:] $$\alpha[t]$$ to achieve high classification accuracy while maintaining operational stability.
To achieve the dual objectives of maximizing classification accuracy and maintaining queue stability, the Lyapunov optimization framework employs a Lyapunov function. This function quantifies the system’s state and stability, providing a basis for decision-making at each time step as,
The quadratic form of L(Q[t]) ensures that deviations from stability are amplified, making it an effective tool for managing queue dynamics. The Lyapunov drift quantifies the expected change in the Lyapunov function over a single time step as,
where [TeX:] $$\Delta(Q[t])$$ represents how the queue backlog evolves over time, given the current state Q[t]. By minimizing the Lyapunov drift, the system reduces the likelihood of queue overload while maintaining stability. To simultaneously address the objectives of accuracy maximization and queue stability, the drift-plus-penalty (DPP) approach is used [31]–[36]. The DPP combines the Lyapunov drift with a penalty term that accounts for classification accuracy,
where V > 0 is a control parameter that balances the tradeoff between classification accuracy and queue stability. The Lyapunov drift is bounded to simplify decision-making is as follows,
(20)
[TeX:] $$\Delta(Q[t]) \leq \frac{1}{2}\left(a[t]^2+b(\alpha[t])^2\right)+Q[t] \cdot(a[t]-b(\alpha[t])) .$$The DPP framework aims to minimize the upper bound of the drift-plus-penalty function, which is equivalent to,
The optimization problem is solved by selecting the MSQCNN configuration [TeX:] $$\alpha[t]$$ at each time step t to maximize as follows,
(22)
[TeX:] $$\alpha[t+1] \leftarrow \arg \max _{\alpha[t] \in \mathcal{A}}[V \cdot \zeta(\alpha[t])+Q[t] b(\alpha[t])],$$where [TeX:] $$\mathcal{A} \text { and } \alpha[t]$$ are the set of all possible MS-QCNN configurations and the optimal configuration at time t, respectively. By leveraging the Lyapunov function and DPP framework, the system ensures dynamic, real-time adjustments to the MSQCNN configuration. This approach balances computational efficiency and classification performance, guaranteeing stable and effective operation in real-world scenarios such as autonomous driving. Furthermore, this method enables the system to prioritize tasks requiring high accuracy during lowload conditions while ensuring system stability during periods of high data influx [37], [38]. As a result, the framework demonstrates scalability and robustness, making it suitable for adaptive decision-making in complex, resource-constrained environments.
TABLE I
| Parameter | Value |
|---|---|
| Quantum simulator | TorchQuantum |
| Qubits per quantum filter | 4 |
| Measurement basis | Pauli-Z |
| MS-QCNN parameter(γ) | 1,2,3 |
| Number of training epochs | 50 |
| Learning rate | 0.001 |
| Parameterized quantum circuit | U3CU3 layer |
| Utility-backlog tradeoff (V) | 20000 |
| Task arrival rate | 13 tasks/slot |
III. PERFORMANCE EVALUATION
The performance of the proposed Lyapunov optimizationbased MS-QCNN selection framework is evaluated through simulations that analyze classification accuracy, queue backlog behavior, and the tradeoff associated with different MS-QCNN stage depths γ. The results are presented using a combination of graphs and tables to highlight the system’s adaptability and efficiency under varying conditions.
A. Evaluation Setup
The proposed algorithm is conducted using an Intel i9- 10990k processor, two NVIDIA Titan X GPUs, and 128GB of RAM. The software environment comprises Python version 3.8.10, alongside quantum computing simulation libraries torchquantum v0.1.5 [39] and PyTorch version 1.8.2 LTS. The evaluation was carried out on the MNIST dataset, which is a well-known benchmark in image recognition, consisting of 70,000 grayscale images of handwritten digits ranging from 0 to 9. The dataset is divided into 60,000 training samples and 10,000 test samples, with each image having a resolution of 28 × 28 pixels. Although the MNIST dataset is relatively simple, it is commonly used in the early stages of model development to validate fundamental image recognition capabilities and computational feasibility. In the context of this study, MNIST serves as a foundational dataset for verifying the effectiveness of the proposed framework, particularly in handling basic image classification tasks. This is especially relevant as accurate image recognition is a critical component of autonomous driving systems, including tasks such as road sign detection and object identification. Therefore, initial validation on MNIST provides essential insights into the model’s fundamental image analysis performance.
B. Evaluation Results
Table II presents the evaluation results highlighting the tradeoffs between classification accuracy and inference time across different MS-QCNN stage depths (γ). The findings demonstrate the inherent relationship between the depth of the MS-QCNN architecture and its computational and classification performance. For γ = 1, the MS-QConv achieves the shortest inference time of 0.08 seconds but the lowest accuracy (88.21%), reflecting the reduced computational demands of a shallow architecture. Increasing the depth to γ = 2 results in a balanced tradeoff, with improved accuracy (94.07%) and moderate inference time of 0.18 seconds. The deepest configuration, γ = 3, offers the highest accuracy (98.01%) but requires the longest inference time, 0.32 seconds. These findings highlight the necessity of dynamic stage depth selection, such as through the Lyapunov optimization framework, to achieve optimal performance based on real-time system requirements.
TABLE II
| Model | Accuracy | Inference Time |
|---|---|---|
| MS-QConv(γ=1) | 88.21 | 0.18 |
| MS-QConv(γ=2) | 94.07 | 0.32 |
| MS-QConv(γ=3) | 98.01 | 0.80 |
The performance of the proposed Lyapunov optimizationbased MS-QCNN framework is evaluated in terms of queue backlog stabilization and classification accuracy, as shown in Figs. 3 and 4. The results highlight the framework’s ability to dynamically balance computational efficiency and classification performance by adapting the MS-QCNN stage. Fig. 3 is the queue backlog dynamics Q[t] over time for the proposed method and fixed MS-QCNN configurations (γ = 1, 2, 3). The adaptive mechanism of the proposed Lyapunov optimizationbased framework ensures gradual queue backlog growth, maintaining stability even under fluctuating arrival rates. In this framework, the γ value is not fixed but dynamically selected in real-time based on the current system state, including queue backlog and computational efficiency. As a result, there is no single, static optimal γ value, but rather a continuously adaptive selection process that optimizes performance throughout the experiment. In contrast, γ = 1 maintains the smallest queue backlog, as the shallow configuration processes tasks quickly. However, this approach is inefficient as it fails to fully utilize the available queue resources, limiting its ability to balance computational efficiency with classification accuracy. For γ = 2, the system demonstrates steady backlog growth while balancing moderate processing speed and classification performance. However, it fails to efficiently use the queue, leading to a gradual increase in backlog over time, which can result in delayed task processing under sustained system loads. This configuration provides moderate efficiency, making it an effective middle ground for scenarios with constrained resources. On the other hand, γ = 3 incurs the highest queue backlog due to the computational demands of deeper feature extraction. While this configuration achieves the highest classification accuracy, it is inefficient for resource-constrained environments, where maintaining low latency is crucial.
Fig. 3.
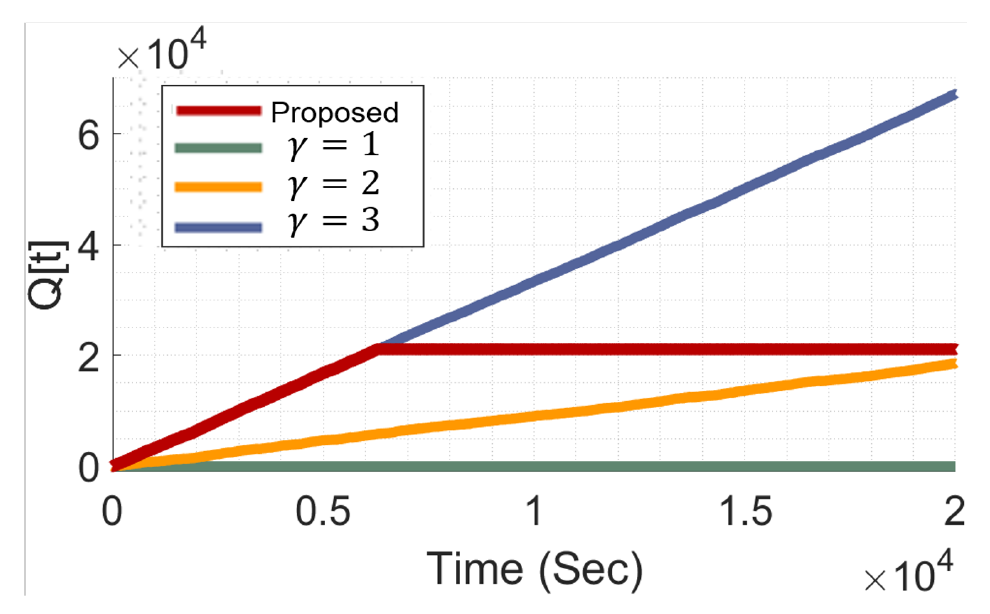
Fig. 4.
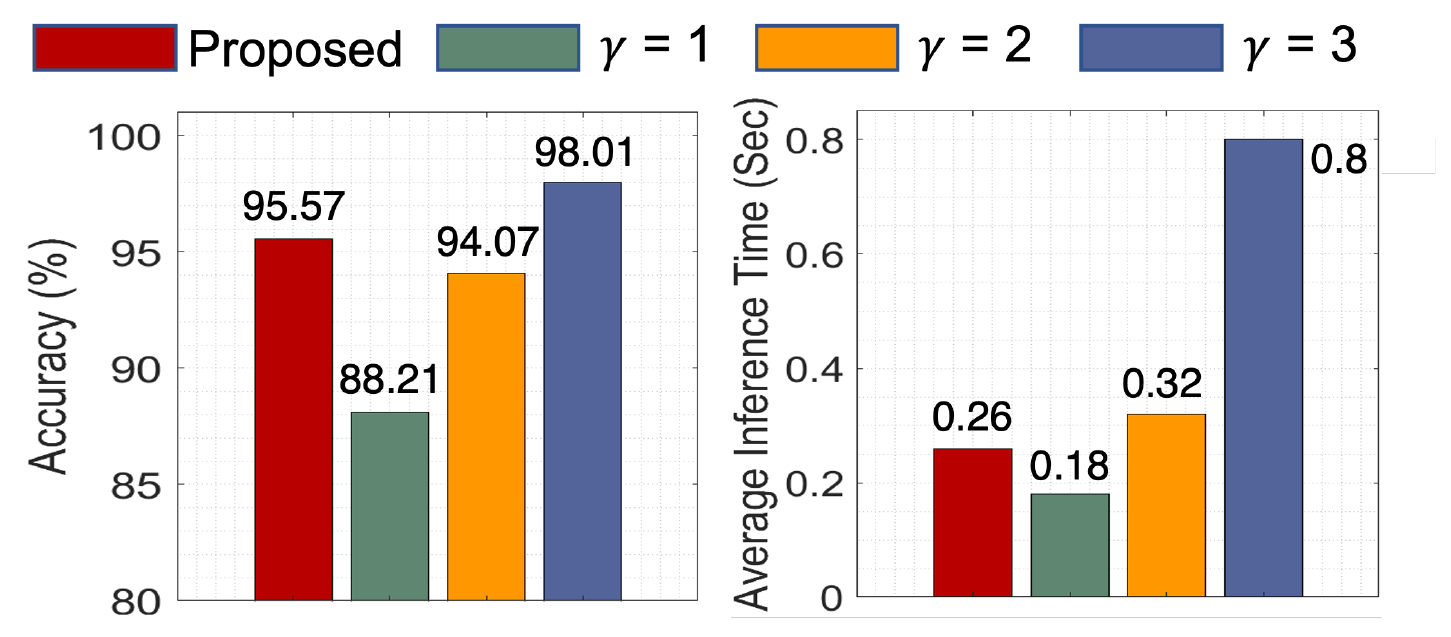
The classification accuracy and inference time comparison presented in Fig. 4 highlights the effectiveness of the proposed Lyapunov optimization-based MS-QCNN framework in balancing computational efficiency with classification performance. By dynamically adjusting the stage depth (γ) based on real-time system conditions, the proposed framework achieves a classification accuracy of 95.57%, demonstrating its adaptability in maintaining high performance while optimizing computational resource utilization. In contrast, fixed MSQCNN configurations exhibit performance tradeoffs dependent on the chosen stage depth. The configurations with γ = 1 and γ = 2 achieve lower accuracy (88.21% and 94.07%, respectively) and are unable to fully optimize the balance between accuracy and efficiency due to their static nature. While γ = 3 achieves the highest accuracy (98.01%) due to deeper feature extraction, this comes at the cost of significantly higher inference time (0.8 seconds), making it less suitable for latency-sensitive and resource-constrained environments. The proposed framework outperforms fixed configurations with γ = 1 and γ = 2 by leveraging dynamic stage selection to optimize accuracy and computational demands in real-time. Furthermore, compared to γ = 3, the proposed framework achieves near-optimal accuracy while substantially reducing inference time, demonstrating its suitability for real-world applications requiring real-time decision-making. This dynamic adaptability ensures that the proposed framework efficiently meets the requirements of varying operational scenarios while delivering robust classification performance.
IV. CONCLUDING REMARKS AND FUTURE WORK
This paper presents the Lyapunov optimization-based framework for the adaptive selection of MS-QCNN configurations in real-time classification tasks, such as those required in autonomous driving systems. The proposed framework dynamically adjusts the stage depth parameter γ of the MS-QCNN to balance computational efficiency and classification accuracy while maintaining system stability through queue management. The performance evaluation demonstrates that the framework effectively manages the tradeoff between accuracy and resource utilization, ensuring queue stability even under high data arrival rates. The results validate the robustness and scalability of the approach, highlighting its suitability for realtime applications in resource-constrained environments.
While the proposed framework demonstrates significant potential, several avenues for future research remain. Given that the current quantum computing landscape is constrained by the NISQ era, the evaluation in this paper is necessarily limited to small-scale datasets, such as MNIST, and restricted choices for the γ parameter. To overcome these limitations, future research should focus on two key aspects. First, further validation of the proposed algorithm in diverse autonomous driving scenarios is required to assess its adaptability and generalizability. Second, deploying the algorithm on actual quantum hardware is necessary to empirically verify its potential advantage over classical algorithms in terms of inference speed. Addressing these aspects would provide deeper insights into the practical applicability of MS-QCNN in real-time decision-making tasks.
Biography
Emily Jimin Roh
Emily Jimin Roh is currently pursuing a Ph.D. degree in Electrical and Computer Engineering at Korea University, Seoul, Republic of Korea. She received a B.S. degree in Intelligent Mechatronics Engineering with a major in Unmanned Vehicle Engineering from Sejong University, Seoul, Republic of Korea, in 2024. Her research focuses include deep learning algorithms, quantum machine learning, and their applications to mobility and networking. She was a Recipient of Bronze Paper Award from IEEE Seoul Section Student Paper Contest (2024).
Biography
Soohyun Park
Soohyun Park has been an Assistant Professor at Sookmyung Women’s University, Seoul, Korea, since March 2024. She was a Postdoctoral Scholar at the Department of Electrical and Computer Engineering, Korea University, Seoul, Korea, from September 2023 to February 2024, where she received her Ph.D. in Electrical and Computer Engineering, in August 2023. She also received her B.S. in Computer Science and Engineering from ChungAng University, Seoul, Korea, in February 2019. Her research interests are in deep learning theory and network/mobility applications, quantum neural network (QNN) theory and applications, QNN software engineering and programming languages, and AIbased autonomous control for distributed computing systems. She was a Recipient of ICT Express Best Reviewer Award (2021), IEEE Seoul Section Student Paper Contest Awards, and IEEE Vehicular Technology Society (VTS) Seoul Chapter Awards.
Biography
Soyi Jung
Soyi Jung has been an Assistant Professor at the Department of Electrical of Computer Engineering, Ajou University, Suwon, Republic of Korea, since September 2022. Before joining Ajou University, she was an Assistant Professor at Hallym University, Chuncheon, Republic of Korea, from 2021 to 2022; a Visiting Scholar at Donald Bren School of Information and Computer Sciences, University of California, Irvine, CA, USA, from 2021 to 2022; a Research Professor at Korea University, Seoul, Republic of Korea, in 2021; and a Researcher at Korea Testing and Research (KTR) Institute, Gwacheon, Republic of Korea, from 2015 to 2016. She received her B.S., M.S., and Ph.D. degrees in Electrical and Computer Engineering from Ajou University, Suwon, Republic of Korea, in 2013, 2015, and 2021, respectively. She was a Recipient of Best Paper Award by KICS (2015), Young Women Researcher Award by WISET and KICS (2015), Bronze Paper Award from IEEE Seoul Section Student Paper Contest (2018), ICT Paper Contest Award by Electronic Times (2019), IEEE ICOIN Best Paper Award (2021), and IEEE Vehicular Technology Society (VTS) Seoul Chapter Awards (2021, 2022).
Biography
Joongheon Kim
Joongheon Kim (M’06-SM’18) has been with Korea University, Seoul, Korea, since 2019, where he is currently an Associate Professor at the School of Electrical Engineering and adjunct professor at the Department of Communications Engineering and Department of Semiconductor Engineering. He also has been a Director for Net-Zero CAFE (Connectivity and Autonomy for Future Ecosystem) Research Center, sponsored by Korean Ministry of Science and ICT (MSIT), since 2024. He received the B.S. and M.S. degrees in Computer Science and Engineering from Korea University, Seoul, Korea, in 2004 and 2006; and the Ph.D. degree in Computer Science from the University of Southern California (USC), Los Angeles, CA, USA, in 2014. Before joining Korea University, he was a Research Engineer with LG Electronics (Seoul, Korea, 2006-2009), a Systems Engineer with Intel Corporation (Santa Clara, CA, USA, 20132016), and an Assistant Professor with Chung-Ang University (Seoul, Korea, 2016-2019). He serves as an Editor for IEEE TRANS. VEHICULAR TECHNOLOGY and IEEE INTERNET OF THINGS JOURNAL. He was a Recipient of Annenberg Graduate Fellowship with his Ph.D. admission from USC (2009), Intel Corporation Next Generation and Standards (NGS) Division Recognition Award (2015), IEEE SYSTEMS JOURNAL Best Paper Award (2020), IEEE ComSoc Multimedia Communications Technical Committee (MMTC) Outstanding Young Researcher Award (2020), and IEEE ComSoc MMTC Best Journal Paper Award (2021). He also received several awards from IEEE conferences including IEEE ICOIN Best Paper Award (2021), IEEE ICTC Best Paper Award (2022), and IEEE Vehicular Technology Society (VTS) Seoul Chapter Awards.
References
- 1 H. Liu et al., "High-precision real-time autonomous driving target detection based on YOLOv8," J. Real-Time Image Process., vol. 21, no. 5, p. 174, Sep. 2024.custom:[[[-]]]
- 2 F. Sultana, A. Sufian, and P. Dutta, "A review of object detection models based on convolutional neural network," Intelligent Computing: Image Processing based Applications, pp. 1-16, Jun. 2020.custom:[[[-]]]
- 3 W. J. Yun, S. Park, J. Kim, and D. Mohaisen, "Self-configurable stabilized real-time detection learning for autonomous driving applications," IEEE Trans. Intell. Transp. Syst., vol. 24, no. 1, pp. 885-890, Jan. 2023.custom:[[[-]]]
- 4 Y . Xiao, X. Zhang, X. Xu, X. Liu, and J. Liu, "Deep neural networks with koopman operators for modeling and control of autonomous vehicles," IEEE Trans. Intell. Veh., vol. 8, no. 1, pp. 135-146, Jan. 2023.custom:[[[-]]]
- 5 S. Ren, K. He, R. B. Girshick, and J. Sun, "Faster R-CNN: Towards real-time object detection with region proposal networks," IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 6, pp. 1137-1149, Jun. 2017.custom:[[[-]]]
- 6 C. Gianoglio, E. Ragusa, P. Gastaldo, and M. Valle, "Trade-off between accuracy and computational cost with neural architecture search: A novel strategy for tactile sensing design," IEEE Sensors Lett., vol. 7, no. 5, pp. 1-4, May 2023.custom:[[[-]]]
- 7 J. Cao, T. Zhang, L. Hou, and N. Nan, "An improved YOLOv8 algorithm for small object detection in autonomous driving," J. Real-Time Image Process., vol. 21, no. 4, p. 138, Jul. 2024.custom:[[[-]]]
- 8 Y . Wu, B. Jiu, Z. Guo, and H. Liu, "Space-time adaptive processing via fast environment sensing," in Proc. IEEE ICSPCC, 2022.custom:[[[-]]]
- 9 S. Park, J. P. Kim, C. Park, S. Jung, and J. Kim, "Quantum multiagent reinforcement learning for autonomous mobility cooperation," IEEE Commun. Mag., vol. 62, no. 6, pp. 106-112, Jun. 2024.custom:[[[-]]]
- 10 I. Kerenidis, J. Landman, and A. Prakash, "Quantum algorithms for deep convolutional neural networks," in Proc. ICLR, 2020.custom:[[[-]]]
- 11 H. Baek, S. Park, and J. Kim, "Logarithmic dimension reduction for quantum neural networks," in Proc. ACM CIKM, 2023.custom:[[[-]]]
- 12 H. Baek, W. J. Yun, S. Park, and J. Kim, "Stereoscopic scalable quantum convolutional neural networks," Neural Netw., vol. 165, pp. 860-867, Aug. 2023.custom:[[[-]]]
- 13 E. J. Roh, H. Baek, D. Kim, and J. Kim, "Fast quantum convolutional neural networks for low-complexity object detection in autonomous driving applications," IEEE Trans. Mobile Comput., vol. 24, no. 2, pp. 1031-1042, Feb. 2025.custom:[[[-]]]
- 14 I. Cong, S. Choi, and M. D. Lukin, "Quantum convolutional neural networks," Nature Physics, vol. 15, no. 12, pp. 1273-1278, Aug. 2019.custom:[[[-]]]
- 15 J. A. Moreno and M. Osorio, "Strict Lyapunov functions for the super-twisting algorithm," IEEE Trans. Autom. Control, vol. 57, no. 4, pp. 1035-1040, 2012.custom:[[[-]]]
- 16 C. Wu, "Lyapunov stability theory for Caputo fractional order systems: The system comparison method," IEEE Trans. Circuits and Syst. II: Express Briefs, vol. 71, no. 6, pp. 3196-3200, Jun. 2024.custom:[[[-]]]
- 17 R. Lian, Z. Li, W. Li, J. Ge, and L. Li, "Predictive vehicle stability assessment using Lyapunov exponent under extreme conditions," IEEE Trans. Intell. Transp. Syst., vol. 25, no. 12, pp. 21559-21571, Dec. 2024.custom:[[[-]]]
- 18 M. Mao, D. Gui, and T. W. S. Chow, "Territory division Lyapunov controller for fast maximum power point tracking of pavement PV system," IEEE Trans. Ind. Electron., vol. 72, no. 1, pp. 536-546, Jan. 2025.custom:[[[-]]]
- 19 M. Choi, W. J. Yun, S. B. Son, S. Park, and J. Kim, "Joint delay-sensitive and power-efficient quality control of dynamic video streaming using adaptive super-resolution," IEEE Trans. Green Commun. Netw., vol. 8, no. 1, pp. 103-117, Mar. 2024.custom:[[[-]]]
- 20 G. Chen et al., "Quantum convolutional neural network for image classification," Pattern Anal. Appl., vol. 26, no. 2, pp. 655-667, Sep. 2023.custom:[[[-]]]
- 21 C. S. Rohwedderetal., "Pooling acceleration in the DaVinci architecture using Im2col and Col2im instructions," in Proc. IEEE IPDPS, 2021.custom:[[[-]]]
- 22 M. Schuld, R. Sweke, and J. J. Meyer, "Effect of data encoding on the expressive power of variational quantum-machine-learning models," Physical Review A, vol. 103, no. 3, p. 032430, Mar. 2021.custom:[[[-]]]
- 23 H. Zhang, T. Li, and F. Li, "Joint mitigation of quantum gate and measurement errors via the z-mixed-state expression of the Pauli channel," Quantum Inf. Process., vol. 23, no. 6, p. 213, May 2024.custom:[[[-]]]
- 24 R. Goebel, "Discrete-time switching systems as difference inclusions: Deducing converse Lyapunov results for the former from those for the latter," IEEE Trans. Autom. Control, vol. 68, no. 6, pp. 3694-3697, Jun. 2023.custom:[[[-]]]
- 25 D. Chen, X. Liu, K. Shi, J. Yang, and N. Tashi, "A necessary and sufficient stability condition of discrete-time monotone systems: A maxseparable Lyapunov function method," IEEE Trans. Circuits Syst. II: Express Briefs, vol. 71, no. 1, pp. 276-280, Jan. 2024.custom:[[[-]]]
- 26 Y . Jia, C. Zhang, Y . Huang, and W. Zhang, "Lyapunov optimization based mobile edge computing for internet of vehicles systems," IEEE Trans. Commun., vol. 70, no. 11, pp. 7418-7433, Nov. 2022.custom:[[[-]]]
- 27 Y . Zhang et al., "Barrier Lyapunov function-based safe reinforcement learning for autonomous vehicles with optimized backstepping," IEEE Trans. Neural Netw. Learn. Syst., vol. 35, no. 2, pp. 2066-2080, Feb. 2024.custom:[[[-]]]
- 28 J. Liu, J. Liu, R. Yan, and T. Ding, "Deep Lyapunov learning: Embedding the Lyapunov stability theory in interpretable neural networks for transient stability assessment," IEEE Trans. Power Syst., vol. 39, no. 6, pp. 7437-7440, Nov. 2024.custom:[[[-]]]
- 29 R. C. Rafaila, C. F. Caruntu, and G. Livint, "Centralized model predictive control of autonomous driving vehicles with Lyapunov stability," in Proc. ICSTCC, 2016.custom:[[[-]]]
- 30 J. Huang, L. Golubchik, and L. Huang, "When Lyapunov drift based queue scheduling meets adversarial bandit learning," IEEE/ACM Trans. Netw., vol. 32, no. 4, pp. 3034-3044, Aug. 2024.custom:[[[-]]]
- 31 J. Koo, J. Yi, J. Kim, M. A. Hoque, and S. Choi, "Seamless dynamic adaptive streaming in LTE/Wi-Fi integrated network under smartphone resource constraints," IEEE Trans. Mobile Comput., vol. 18, no. 7, pp. 1647-1660, Jul. 2019.custom:[[[-]]]
- 32 J. Kim, G. Caire, and A. F. Molisch, "Quality-aware streaming and scheduling for device-to-device video delivery," IEEE/ACM Trans. Netw., vol. 24, no. 4, pp. 2319-2331, Aug. 2016.custom:[[[-]]]
- 33 S. Jung, J. Kim, and J.-H. Kim, "Intelligent active queue management for stabilized QoS guarantees in 5G mobile networks," IEEE Syst. J., vol. 15, no. 3, pp. 4293-4302, Sep. 2020.custom:[[[-]]]
- 34 J. Koo, J. Yi, J. Kim, M. A. Hoque, and S. Choi, "REQUEST: Seamless dynamic adaptive streaming over HTTP for multi-homed smartphone under resource constraints," in Proc. ACM MM, 2017.custom:[[[-]]]
- 35 M. J. Neely, Stochastic Network Optimization with Application to Communication and Queueing Systems, ser. Synthesis Lectures on Communication Networks. Morgan Claypool Publishers, 2010.custom:[[[-]]]
- 36 S. Jung, J. Kim, M. Levorato, C. Cordeiro, and J.-H. Kim, "Infrastructure-assisted on-driving experience sharing for millimeterwave connected vehicles," IEEE Trans. Veh. Technol., vol. 70, no. 8, pp. 7307-7321, Aug. 2021.custom:[[[-]]]
- 37 R. Xie et al., "Delay-prioritized and reliable task scheduling with long-term load balancing in computing power networks," IEEE Trans. Services Comput., pp. 1-14, 2024 (Early Access).custom:[[[-]]]
- 38 J. Zhang, Y . Zhai, Z. Liu, and Y . Wang, "A Lyapunov-based resource allocation method for edge-assisted industrial internet of things," IEEE Internet Things J., vol. 11, no. 24, pp. 39464-39472, Dec. 2024.custom:[[[-]]]
- 39 H. Wang et al., "QOC: Quantum on-chip training with parameter shift and gradient pruning," in Proc. IEEE/ACM Des. Autom. Conference, 2022.custom:[[[-]]]